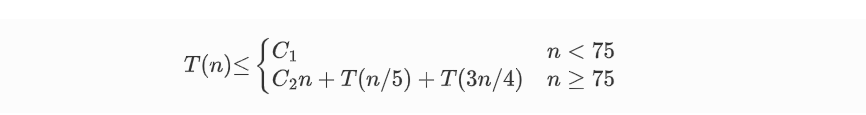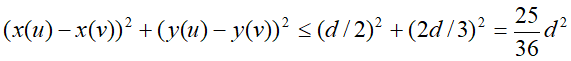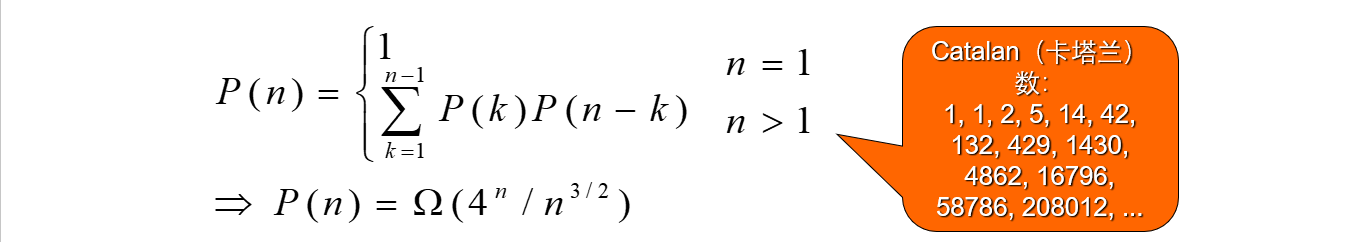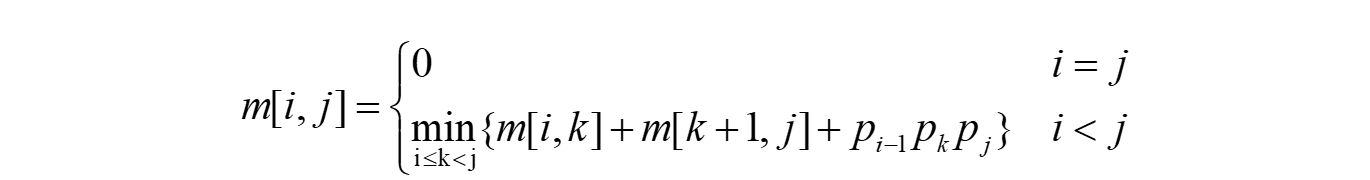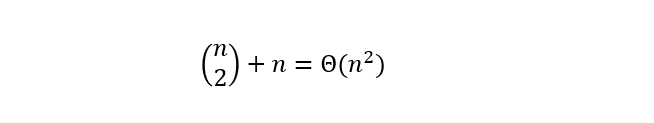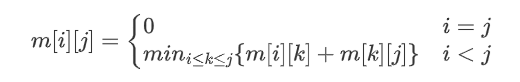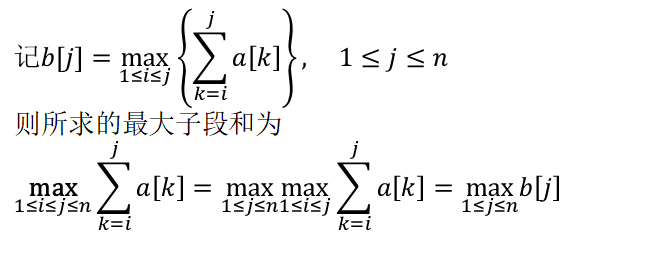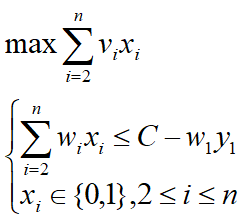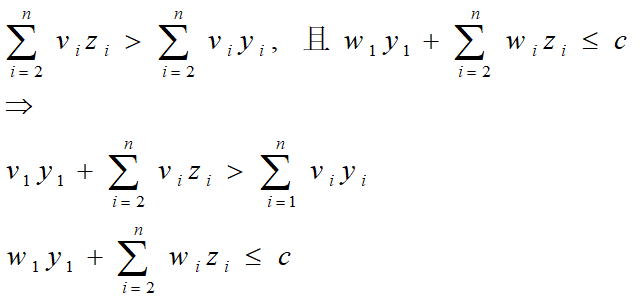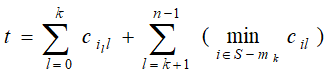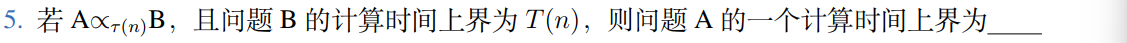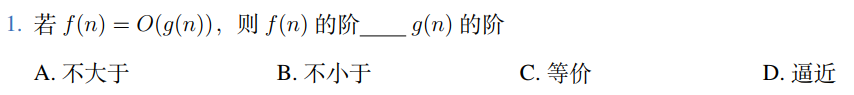算法设计与分析 #
1.课太蠢,简单写一点复习笔记
2.大量的数学笔记都是我复制下来的,我没有手打这么多公式的耐心,只能感谢那名陌生的同学了,原来的仓库https://github.com/DANNHIROAKI/XJTU-CS-Courses/tree/master,可能这篇文章的阅读体验相对会更好一点,因为数学公式会直接渲染并且我会多余做一些补充和更改,如果原作者看到并且觉得这样不好,您可以直接联系我删除。
3.代码就会按照原书中来的,利用Java来实现。
4.https://csdiy.wiki/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95/CS170/ 笔者非常后悔在学校老师狂念PPT的时候没有自学这个CS170,如果你还有机会,一定要看一看。
5.关于本课程你理论上能找到两套往年题目,有参考价值,模拟题目参考价值较少,本课程从选修变成必修之后难度应当有所降低,不管你的老师怎么样,考试之前的复习课一定去听,会透露原题。
1.算法概述 #
算法的执行次数和时间都有限。程序不一定,因为有可能有while(true)。
时间复杂性问题 #
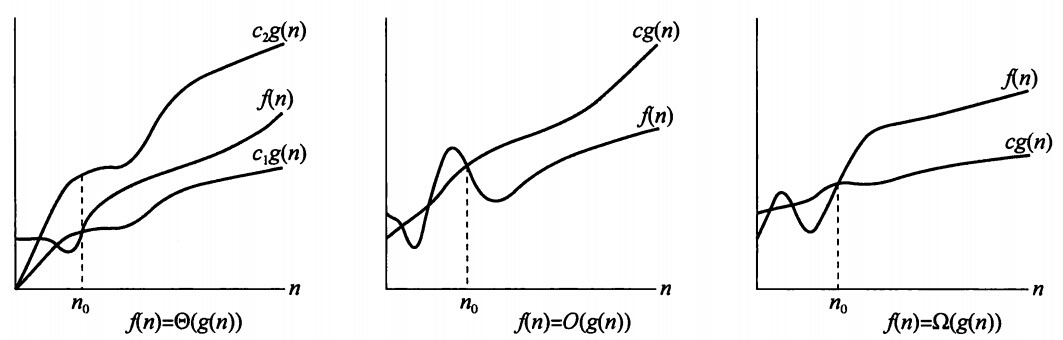
O omu o theta

举例子:
f = O(g)
g是f的一个上界,f <= g
omu: >=
o: <
theta: = (既是O 又是omu)
omega: >
n的阶乘
Stirling’s approximation 是对n !趋于无穷速度的估计,公式如下
𝑛!=2𝜋𝑛(𝑛𝑒𝑛)(1+Θ(1𝑛))
可推导:
𝑛!=𝑜(𝑛𝑛) 𝑛!=𝜔(2𝑛) log(𝑛!)=Θ(𝑛log𝑛)
课后题证明以及上下界的练习。
渐进分析的算术运算与证明
应该不难,想办法凑就可以。
常用公式:
•O(f(n))+O(g(n)) = O(max{f(n),g(n)}) ;
•O(f(n))+O(g(n)) = O(f(n)+g(n)) ;
•O(f(n))O(g(n)) = O(f(n)*g(n)) ;
•O(cf(n)) = O(f(n)) ;
•g(n)= O(f(n)) ⇒ O(f(n))+O(g(n)) = O(f(n))
证明示例:以第一个公式举例
•规则O(f(n)) + O(g(n)) = O(max{f(n),g(n)}) 的证明:
•对于任意f1(n)∈ O(f(n)) ,存在正常数c1和自然数n1,使得对所有n ≥ n1,有f1(n)≤c1f(n) 。
•类似地,对于任意g1(n)∈ O(g(n)) ,存在正常数c2和自然数n2,使得对所有n ≥ n2,有g1(n) ≤ c2g(n) 。
•令c3=max{c1, c2}, n3 =max{n1, n2},h(n)= max{f(n),g(n)} 。
•则对所有的 n ≥ n3,有
•f1(n) +g1(n) ≤ c1f(n) + c2g(n)
≤ c3f(n) + c3g(n)= c3(f(n) + g(n))
≤ c3×2 max{f(n),g(n)}
= 2c3h(n)
则有f1(n) +g1(n)=O(h(n))= O(max{f(n),g(n)})
即O(f(n))+O(g(n)) = O(max{f(n),g(n)})
能搞清楚上下界就没问题。
NP问题 #
应该会考相关的归约的方法。
概括 #
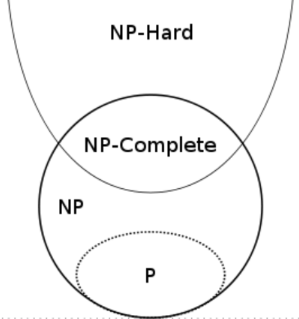
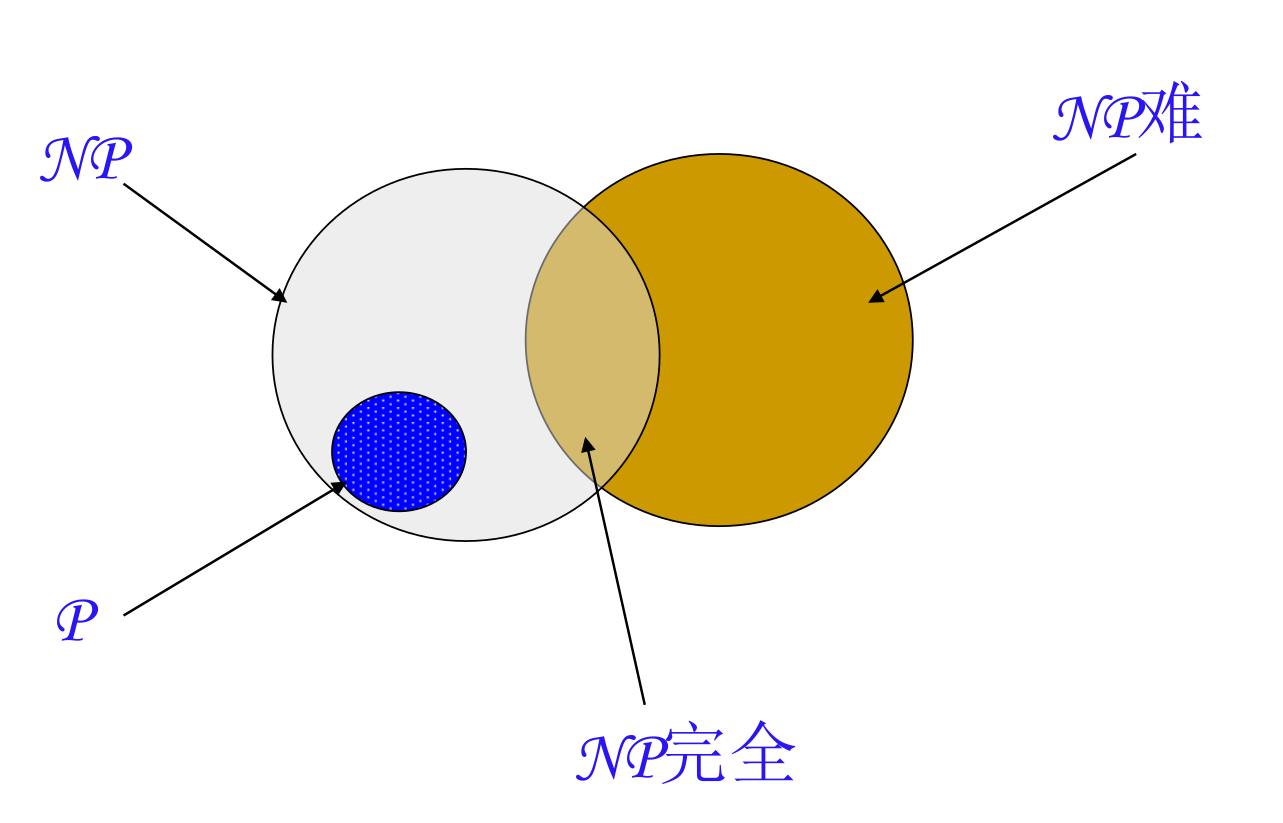
- P:可以“快速解决”的问题(即,多项式时间内能求解)。
- NP:可以“快速验证答案”的问题。
- NPC(NP-Complete,NP 完全):目前认为“最难的 NP 问题”,一旦能快速解决一个,就能快速解决所有 NP 问题。
- NP-hard(NP 困难):至少跟 NP 中最难的问题一样难,但本身不一定属于 NP。
解释 #
注意这张图的关系:
P(Polynomial Time)问题 #
- 定义:能在“多项式时间”内求出解的问题。
- 理解方式:你的程序运行时间是 O(n),O(n2),O(n3)O(n), O(n^2), O(n^3)O(n),O(n2),O(n3) 这种(不是指数或阶乘),就属于 P。
- 例子:
- 排序(冒泡、快排)
- 最短路径(Dijkstra)
- 匹配括号是否合法(栈)
NP(Non-deterministic Polynomial Time)问题 #
- 定义:解可以在多项式时间内被验证的问题。
- 关键点:你不一定能很快找到解,但一旦别人告诉你答案,你可以很快验证它对不对。
- 例子:
- 给一个图,问是否存在一个旅行路径经过所有城市一次?(TSP)
- 给一个布尔表达式,问是否存在变量组合使其为真?(SAT)
NP 完全(NPC, NP-Complete) #
- 定义:NP 中最难的问题。
- 满足两个条件:
- 本身属于 NP。
- 所有 NP 问题都可以在多项式时间归约到它上。
- 通俗理解:它是“NP 阶层中的老大哥”。如果有一天你能快速解决一个 NPC 问题,那你就能快速解决所有 NP 问题(即 P=NPP = NPP=NP)。
- 著名例子:
- SAT(布尔可满足性问题)
- TSP(旅行商问题)
- 3-Coloring(三染色问题)
- Subset Sum(子集和问题)
NP-hard(NP 困难) #
注意:NP难问题不一定是NP问题!
- 定义:比 NP 还难的问题(不一定能验证解)。
- 不一定在 NP 类别中,比如不要求答案验证要快。
- 一些 NP-hard 问题甚至不可判定(比如停机问题)。
2.递归和分治策略 #
凡治众如治寡,分数是也。 —-《孙子兵法》
求解采用自顶向下的计算方式。
1.最优子结构。2.小问题可以直接解决。3.最后可以小的问题合并成最终答案。4.子问题之间相互独立。
概念 #
hanoi问题:
设a,b,c是3个塔座。开始时,在塔座a上有一叠共n个圆盘,这些圆盘自下而上,由大到小地叠在一起。各圆盘从小到大编号为1,2,…,n,现要求将塔座a上的这一叠圆盘移到塔座b上,并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则:
规则1:每次只能移动1个圆盘;
规则2:任何时刻都不允许将较大的圆盘压在较小的圆盘之上;
规则3:在满足移动规则1和2的前提下,可将圆盘移至a,b,c中任一塔座上。
void hanoi(int n, int a, int b, int c)
{
if (n > 0)
{
hanoi(n-1, a, c, b); //设法将n-1个较小的圆盘依照移动规则从塔座a移至塔座c
move(a,b); //将塔座a上编号为n的圆盘移到b上
hanoi(n-1, c, b, a); //设法将n-1个较小的圆盘依照移动规则从塔座c移至塔座b
}
}
一般的流程:
void divide-and-conquer(P)
{
if ( | P | <= n0) adhoc(P); //解决小规模的问题
divide P into smaller subinstances P1,P2,...,Pk;//分解问题
for (i=1,i<=k,i++){
yi=divide-and-conquer(Pi);
} //递归的解各子问题
return merge(y1,...,yk); //将各子问题的解合并为原问题的解
}
递归的求解 #
一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。设分解阀值n0=1,且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。
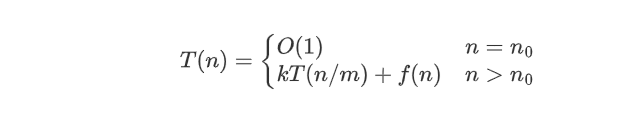

1.递归树法 #
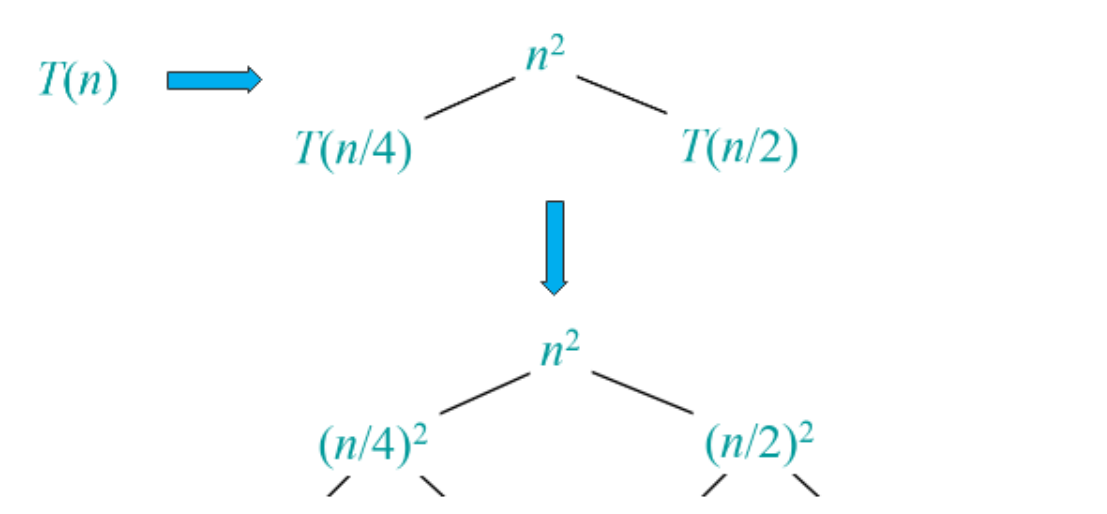
考虑分解和合并的时间:
由于该递归表达式分为两项,所以算树的高度时,我们只需要看n/2的分解,由
𝑛2ℎ=1
可得递归树的层数为
ℎ=log2𝑛
分解的时间消耗为
𝑡1\len2(1+516+25256+…+(516)log2𝑛−1=(516)log2𝑛−1516−1<1611𝑛2
则有
𝑡1=𝑂(𝑛2)
叶子节点小于n个,所以合并就是O(n),那么最终就为t1。
2.主方法 #
令和𝑎≥1和𝑏>1是常数,𝑓(𝑛)是一个函数,𝑇(𝑛)是定义在非负整数上的递归式: 𝑇(𝑛)=𝑎𝑇(𝑛𝑏)+𝑓(𝑛)
T(n) 有如下渐进界:
1️⃣ 若对某个常数 ϵ > 0 有𝑓(𝑛)=𝑂(𝑛log𝑏𝑎−𝜖),则 T ( n ) = Θ (nlogba)
2️⃣ 若𝑓(𝑛)=Θ(𝑛log𝑏𝑎),则𝑇(𝑛)=Θ(𝑛log𝑏𝑎lg𝑛)
3️⃣ 若对某个常数 ϵ > 0 有𝑓(𝑛)=Ω(𝑛log𝑏𝑎+𝜖),且对某个常数𝑐<1和足够大的n有𝑎𝑓(𝑛/𝑏)≤𝑐𝑓(𝑛)则
T ( n ) = Θ ( f ( n ) )
注意点
在第一种情况中,不是𝑓(𝑛)小于𝑛log𝑏𝑎就够了,而是要多项式意义上的小于,也就是说,𝑓(𝑛)必须渐进小于𝑛log𝑏𝑎,要相差一个因子𝑛𝜖。
其中𝜖是大于0的常数。
在第三种情况中,不是𝑓(𝑛)大于𝑛log𝑏𝑎就够了,而是要多项式意义上的大于,而且还要满足"正则"条件𝑎𝑓(𝑛/𝑏)≤𝑐𝑓(𝑛)。遇到的多项式界的函数中,多数都满足这个条件。
此外,这三种情况并非覆盖了𝑓(𝑛)的所有情况,𝑓(𝑛)可能小于𝑛log𝑏𝑎,但不是多项式意义上的小于,也有可能大于但不是多项式意义上的大于,这时候就不能用主方法来求解,而是需要用递归树。
举例说明 #
1️⃣ T (n) = 9 T (n/3) + n
有𝑎=9,𝑏=3,𝑓(𝑛)=𝑛,因此𝑛log𝑏𝑎=𝑛log39=Θ(𝑛2),当我们取𝜖=1,有𝑓(𝑛)=𝑂(𝑛log39−1),由定理一则有𝑇(𝑛)=Θ(𝑛2)
2️⃣ T (n) = T (2n/3) + 1
有𝑎=1,𝑏=3/2,𝑓(𝑛)=1,因此𝑛log𝑏𝑎=𝑛log3/21=𝑛0=Θ(1),由于𝑓(𝑛)=Θ(𝑛log𝑏𝑎)=Θ(1),由定理二则有𝑇(𝑛)=Θ(lg𝑛)
3️⃣ T (n) = 3 T (n/4) + nlgn
有𝑎=3,𝑏=4,𝑓(𝑛)=𝑛lg𝑛,因此𝑛log𝑏𝑎=𝑛log43=𝑂(𝑛0.793),由于𝑓(𝑛)=Ω(𝑛log43+𝜖),其中𝜖≈0.2,因此如果可以证明正则条件成立,则可以使用定理三。当n足够大时,对于𝑐=3/4,(𝑎𝑓(𝑛/𝑏)=3(𝑛/4)lg(𝑛/4)≤(3/4)𝑛lg𝑛=𝑐𝑓(𝑛),由定理二则有𝑇(𝑛)=Θ(𝑛lg𝑛)
⚠️主方法不适用于𝑇(𝑛)+2𝑇(𝑛/2)+𝑛lg𝑛
有𝑎=2,𝑏=2,𝑓(𝑛)=𝑛lg𝑛,因此𝑛log𝑏𝑎=𝑛,𝑓(𝑛)虽然渐进大于n,但是并不是多项式意义上的的大于**(比值要是n的次方)**,对于任意的正常数𝜖,比值𝑓(𝑛)/𝑛log𝑏𝑎=lg𝑛都渐进小于𝑛𝜖,陷入了特殊情况,使用递归树可解决。
可以这么理解,谁大就由谁来决定,相等的情况就是对数和算出来的式子直接做乘法。
分治算法具体问题设计 #
merge and sort
1.二分算法 #
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right){
int mid = left + (right - left) / 2;
if(nums[mid] < target){
left = mid + 1;
}else if(nums[mid] > target){
right = mid - 1;
}else{
return mid;
}
}
return -1;
}
}
每执行一次算法的while循环,待搜索的数组的大小就减少一半。因此,在最坏情况下,while循环被执行了𝑂(log𝑛)次。循环体内运算需要𝑂(1)时间,因此整个算法在最坏情况下的时间复杂性为𝑂(log𝑛)。
二分代码的纠错,写出bugfree的二分代码,分析七个二分算法的错误。

下标变化错误,会进入死循环。(1 2 3 5 6 7 这个序列中去找数字4)

right控制的有问题,当要查找的数据在最右边的时候就找不到了(1 2 3 5 6 7 中找 7)

和上面是同理的,left + 1 != right 就是 left < right - 1


下标控制错误,left = middle + 1,当要查找的元素为数组中的最后一个的时候,此时陷入死循环。

class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left < right){
int mid = left + (right - left) + 1 / 2;
if(nums[mid] < target){
left = mid;
}else if(nums[mid] > target){
right = mid - 1;
}else{
return mid;
}
}
if(target == nums[left]){
return left;
}
return -1;
}
}
第五个是正确的代码,middle控制的向上作取整可以使得left不用等于middle加1,当有多个重复的时候,取的值是最右边的值。

多了right = mid - 1,这样我们就没办法找到最右边的值了。注意这两个代码都是 left < right 而非相等的。
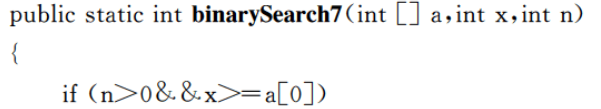

right = mid,右边的值到不了左边来,那么当你找的数字为第一个元素的时候就会陷入死循环。
从判断错误的角度来讲,举极端例子(找最左边或者最右边),或者数组长度只有1的情况都是很好的方法。
2.大整数乘法 #
处理两个位数很大的数字的乘法:
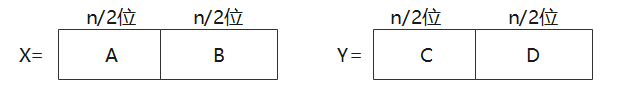

用类似于因式分解的方法,把原来的两次乘法改成一次乘法,但是只是多了几次加法而已。
3.Strassen矩阵乘法 #
这一部分可以看书,把八次乘法转换成了七次的乘法,和上面的大整数乘法是类似的思想。
4.棋盘覆盖问题 #
在一个2𝑘×2𝑘 个方格组成的棋盘中,恰有一个方格与其它方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。

将2𝑘×2𝑘 棋盘分割为4个2𝑘−1×2𝑘−1 子棋盘(a)所示。特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,如 (b)所示,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为棋盘1×1。
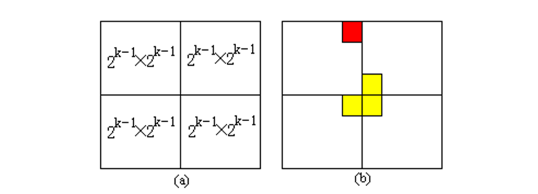
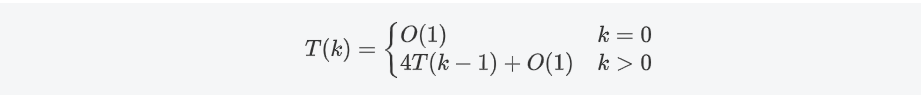
解此递归方程可得𝑇(𝑘)=𝑂(4𝑘),由于覆盖一个2𝑘×2𝑘 棋盘所需要的L型骨牌个数为(4𝑘−1)/3,所以该算法为一个在渐进意义下的最优算法。
5.合并排序(merge sort) #
基本思想:将待排序元素分成大小大致相同的2个子集合,分别对2个子集合进行排序,最终将排好序的子集合合并成为所要求的排好序的集合。
最坏时间复杂度:O(nlogn) 平均时间复杂度:O(nlogn) 辅助空间:O(n)
最坏情况下的时间复杂度:
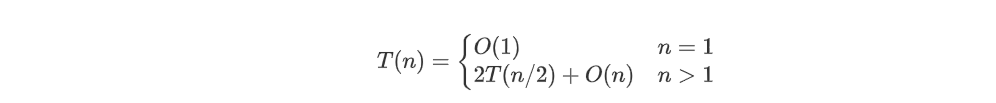
概念:解此递归方程为𝑇(𝑛)=𝑂(𝑛log𝑛),由于排序问题的计算时间下界为Ω(𝑛log𝑛),所以合并排序算法为一个渐进最优算法。
对于算法MergeSort,可以利用分治法消除其中的递归。可以先将数组a中相邻的元素两两配对,用合并算法将他们排序,构成n/2组长度为2的排好序的子数组段,然后再把它们排成长度为4的排好序的子数组段,如此继续下去,直至整个数组排好序。
package Recursion;
public class MergeSort {
private void sortArray(int[] array) {
merge(array, 0, array.length - 1);
}
private void mergeSort(int[] array, int left, int mid, int right) {
int[] temp1 = new int[mid - left + 1];
int[] temp2 = new int[right - mid];
for (int i = 0; i < temp1.length; i++) {
temp1[i] = array[left + i];
}
for (int i = 0; i < temp2.length; i++) {
temp2[i] = array[mid + 1 + i];
}
int i = 0, j = 0;
int k = left;
while (i < temp1.length && j < temp2.length) {
//注意这里保证了排序的稳定性,小于等于就直接放进去
if (temp1[i] <= temp2[j]) {
array[k] = temp1[i];
++i;
++k;
}else{
array[k] = temp2[j];
++j;
++k;
}
}
while (i < temp1.length) {
array[k] = temp1[i];
++i;
++k;
}
while (j < temp2.length) {
array[k] = temp2[j];
++j;
++k;
}
}
private void merge(int[] array, int left , int right){
if(left < right){
int mid = left + (right - left)/2;
merge(array, left, mid);
merge(array, mid + 1, right);
mergeSort(array, left, mid, right);
}
}
public static void main(String[] args) {
int[] array = {9,8,7,6,5,4,3,2,1};
MergeSort mergeSort = new MergeSort();
mergeSort.sortArray(array);
for(int index = 0; index < array.length; index++){
System.out.print(array[index] + " ");
}
}
}
6.快速排序(Quick Sort) #
在快速排序中,记录的比较和交换是从两端向中间进行的,关键字较大的记录一次就能交换到后面单元,关键字较小的记录一次就能交换到前面单元,记录每次移动的距离较大,因而总的比较和移动次数较少。
算法分析如下:
对于输入的子数组a[p:r],按照以下三个步骤排序:
1️⃣ 分解:以a[p]作为基准元素将a[p:r]分解为三段a[p:q-1],a[q],a[q+1:r],使a[p:q-1]中的任意一个元素小于等于a[q],a[q+1:r]中任何一个元素大于等于a[q],下标在划分过程中确定。
2️⃣ 递归求解:通过递归调用快速排序算法,分别对a[p:q-1]和a[q+1:r]进行排序
3️⃣ 合并:由于对a[p:q-1]和a[q+1:r]的排序使就地进行的,因此排好序后不需要再执行其他计算。
package Recursion;
public class QuickSort {
public static void main(String[] args) {
int[] arr = {15,14,13,12,11,10,9,8,7,6,5,4,3,2,1};
quickSort(arr,0,arr.length-1);
for(int a:arr){
System.out.print(a + " ");
}
}
private static void quickSort(int[] arr, int left, int right) {
if(left < right){
int partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex-1);
quickSort(arr, partitionIndex+1, right);
}
}
private static int partition(int[] arr, int left, int right) {
int pivot = arr[left];
while(left < right){
//找到第一个小于pivot的元素
while(left < right && arr[right] >= pivot){
right--;
}
//把右边的值移到左边来
arr[left] = arr[right];
//找到第一个大于pivot的元素
while(left < right && arr[left] <= pivot){
left++;
}
//把左边的值移到右边来
arr[right] = arr[left];
}
//最后进行交换
arr[left] = pivot;
return left;
}
}
这里是取第一个元素作为划分的基准,如果取最后一个元素作为基准而且其是数组中最大的元素,那么会陷入死循环。
对于输入序列a[p:r] , Partition的计算时间显然为𝑂(𝑟−𝑝−1)。
快速排序的运行时间与划分是否对称有关,其最坏情况发生在划分过程产生的两个区域分别包含n- 1个元素和1个元素的时候。由于函数Partition的计算时间为𝑂(𝑛),所以如果算法Partition的每一步都出现这种不对称划分,则其计算时间复杂性T(n) 满足
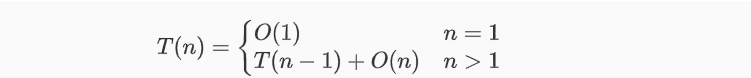
解此递归方程可得𝑇(𝑛)=𝑂(𝑛2)。
在最好情况下,每次划分所取的基准都恰好为中值,即每次划分都产生两个大小为n/2的区域,此时,Partition的计算时间T(n)满足
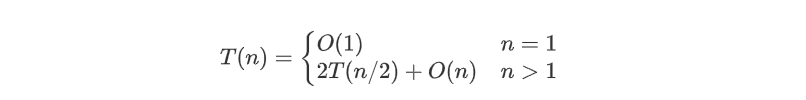
可以证明,快速排序算法在平均情况下的时间复杂性也是 T ( n ) = O ( n log n ) ,这在基于比较的排序算法类中算是快速的,快速排序也因此而得名。
随机选取值而不是每次都选取第一个就可以解决这个问题。
7.线性时间选择 #
⭐ 要能根据代码分析时间复杂度
给定线性序集中n个元素和一个整数k,1≤k≤n,要求找出这n个元素中第k小的元素,只需要调用如下方法:RandomizedSelect(a,0,n-1,k)
template<class Type>
Type RandomizedSelect(Type a[],int p, int r, int k){
if(p==r)
return a[p];
int i = RandomizePartition(a,p,r);
j=i-p+1;
if(k<=j)
return RandomizedSelect(a,p,i,k);
else
return RandomizedSelect(a,i+1,r,k-j);
}
在算法RandomizedSelect中执行RandomizedPartition后;数组a[p:r]被划分成两个子数组a[p:i]和a[i+1:r],使得中每个元素都不大于a[i+1:r]中每个元素。接着算法计算子数组a[p:i]中元素个数j。如果k≤j,则a[p:r]中第k小元素落在子数组a[p:i]中如果k> j,则要找的第k小元素落在子数组a[i+1:r]中。由于此时已知道子数组a[p:i]中元素均小于要找的第k小元素,因此,要找的a[p:r]中第k小元素是a[i+ 1:r]中的第k- j 小元素。
在最坏情况下,算法RandomizedSelect需要𝑂(𝑛2)计算时间。例如在找最小元素时,总是在最大元素处划分。尽管如此,该算法的平均性能很好。在平均情况下,算法RandomizedSelect可以在𝑂(𝑛)时间内解决⭐
如果能在线性时间内找到一个划分基准,使得按这个基准所划分出的2个子数组的长度都至少为原数组长度的ε倍(0<ε<1是某个正常数),那么就可以在最坏情况下用O(n)时间完成选择任务。例如,若ε=9/10,算法递归调用所产生的子数组的长度至少缩短1/10。所以,在最坏情况下,算法所需的计算时间T(n)满足递归式T(n)≤T(9n/10)+O(n) 。由此可得T(n)=O(n)。
寻找划分标准的算法如下:
分组,寻找中位数的中位数,这样的分割位置相对来说比较公平。
1️⃣ 将n个输入元素划分成⌈𝑛/5⌉个组,每组5个元素,只可能有一个组不是5个元素。用任意一种排序算法,将每组中的元素排好序,并取出每组的中位数,共⌈𝑛/5⌉个。
2️⃣ 递归调用Select来找出这⌈𝑛/5⌉个元素的中位数。如果⌈𝑛/5⌉是偶数,就找它的2个中位数中较大的一个。以这个元素作为划分基准。
设所有元素互不相同。在这种情况下,找出的基准x至少比3(n-5)/10个元素大,因为在每一组中有2个元素小于本组的中位数,而n/5个中位数中又有(n/5-1)/2=(n-5)/10个小于基准x。同理,基准x也至少比3(n-5)/10个元素小。而当n≥75时,3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4。
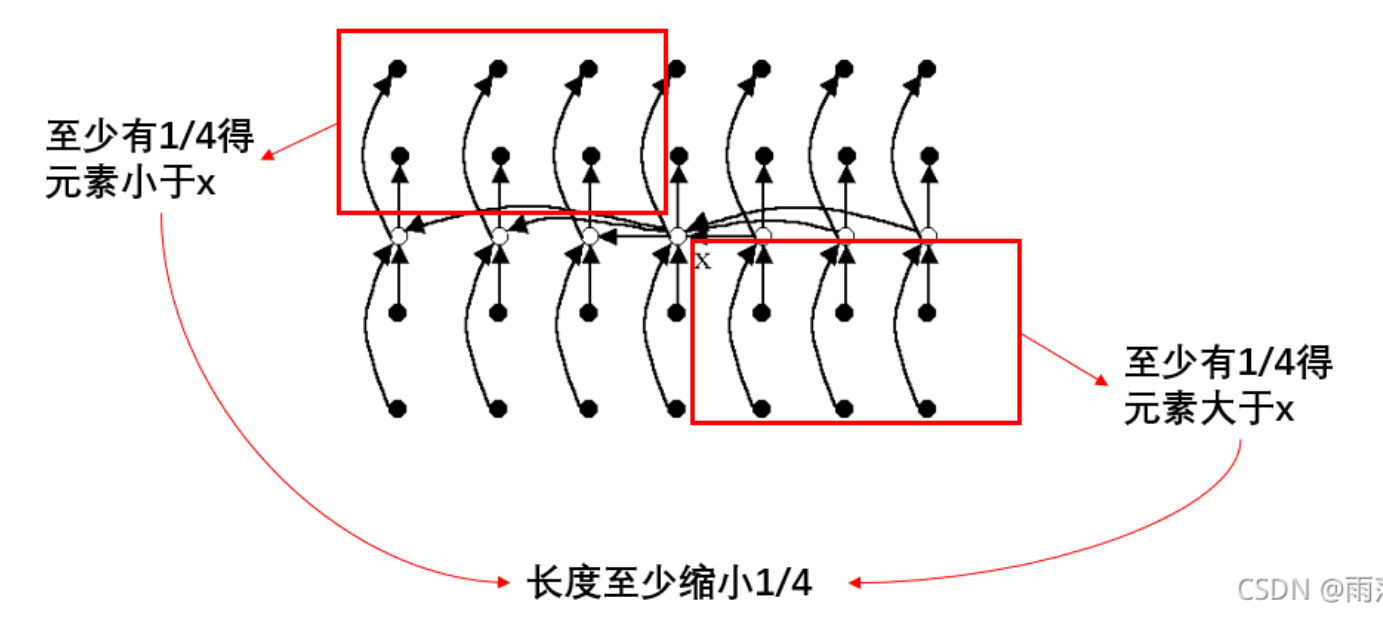
template<class Type>
Type Select(Type a[], int p, int r, int k)
{
if (r-p<75) {
Sort(Type a[], int p, int r);
//用某个简单排序算法对数组a[p:r]排序;
return a[p+k-1];
};
for ( int i = 0; i<=(r-p-4)/5; i++ )
//将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
Type x = Select(a, p, p+(r-p-4)/5, (r-p-4)/10); //找中位数的中位数,r-p-4即上面所说的n-5
int i=Partition(a,p,r, x),
j=i-p+1;
if (k<=j) return Select(a,p,i,k);
else return Select(a,i+1,r,k-j);
}
上述算法将每一组的大小定为5,并选取75作为是否作递归调用的分界点。这2点保证了T(n)的递归式中2个自变量之和n/5+3n/4=19n/20=εn,0<ε<1。这是使T(n)=O(n)的关键之处。当然,除了5和75之外,还有其他选择
解得:𝑇(𝑛)=𝑂(𝑛),要会用递归树求解
看不懂就记住时间复杂度为O(n),考试前再看一下原理,记忆一下数字规律也可以。
8.最近点对问题 #
会写伪代码,典型的简答题。
给定平面上n个点,找其中的一对点,使得在n个点组成的所有点对中,该点对的距离最小。
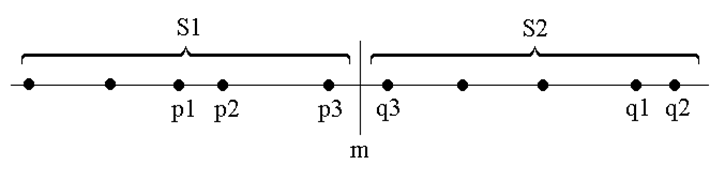
为了使问题易于理解和分析,先来考虑一维的情形。此时,S中的n个点退化为x轴上的n个实数 x1,x2,…,xn。最接近点对即为这n个实数中相差最小的2个实数。
假设我们用x轴上某个点m将S划分为2个子集S1和S2 ,基于平衡子问题的思想,用S中各点坐标的中位数来作分割点。递归地在S1和S2上找出其最接近点对{p1,p2}和{q1,q2},并设d=min{|p1-p2|,|q1-q2|},S中的最接近点对或者是{p1,p2},或者是{q1,q2},或者是某个{p3,q3},其中p3∈S1且q3∈S2。如果S的最接近点对是{p3,q3},即|p3-q3|<d,则p3和q3两者与m的距离不超过d,即p3∈(m-d,m],q3∈(m,m+d]。由于在S1中,每个长度为d的半闭区间至多包含一个点(否则必有两点距离小于d),并且m是S1和S2的分割点,因此(m-d,m]中至多包含S中的一个点。由图可以看出,如果(m-d,m]中有S中的点,则此点就是S1中最大点,同理S2这么找就会找到最小的点。因此,我们用线性时间就能找到区间(m-d,m]和(m,m+d]中所有点,即p3和q3。从而我们用线性时间就可以将S1的解和S2的解合并成为S的解。
以下是二维的情况:
选取一垂直线l:x=m来作为分割直线。其中m为S中各点x坐标的中位数。由此将S分割为S1和S2。递归地在S1和S2上找出其最小距离d1和d2,并设d=min{d1,d2},S中的最接近点对或者是d,或者是某个{p,q},其中p∈P1且q∈P2。
考虑P1中任意一点p,它若与P2中的点q构成最接近点对的候选者,则必有distance(p,q)<d。满足这个条件的P2中的点一定落在一个d×2d的矩形R中由d的意义可知,P2中任何2个S中的点的距离都不小于d。由此可以推出矩形R中最多只有6个S中的点。因此,在分治法的合并步骤中最多只需要检查6×n/2=3n个候选者
⭐ 证明 将矩形R的长为2d的边3等分,将它的长为d的边2等分,由此导出6个(d/2)×(2d/3)的矩形。若矩形R中有多于6个S中的点,则由鸽舍原理易知至少有一个(d/2)×(2d/3)的小矩形中有2个以上S中的点。设u,v是位于同一小矩形中的2个点,则
证明就是六等分,那么一个小矩形的对角边就是最大的长度。
distance(u,v)<d。这与d的意义相矛盾。图b是具有6个S中的点的极端情况。
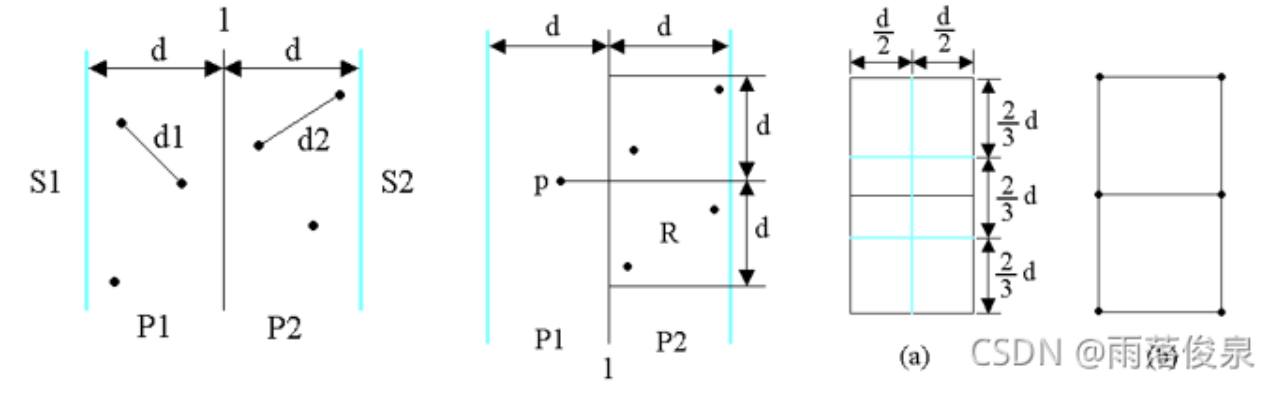
由上述证明可知,在分治法的合并步骤中,最多只需要检查6xn/2=3n个候选者,而不是n^2/4个。
为了确切地知道要检查哪6个点,可以将p和P2中所有S2的点投影到垂直线l上。由于能与p点一起构成最接近点对候选者的S2中点一定在矩形R中,所以它们在直线l上的投影点距p在l上投影点的距离小于d。由上面的分析可知,这种投影点最多只有6个。因此,若将P1和P2中所有S中点按其y坐标排好序,则对P1中所有点,对排好序的点列作一次扫描,就可以找出所有最接近点对的候选者。对P1中每一点最多只要检查P2中排好序的相继6个点。
以下就是伪代码:
double cpair2(S)
{
n=|S|;
if (n < 2) return 无穷;
1、m=S中各点x间坐标的中位数;
//构造S1和S2;
S1={p∈S|x(p)<=m};
S2={p∈S|x(p)>m};
//作递归的处理
2、 d1=cpair2(S1);
d2=cpair2(S2);
//找到集合内的最近距离点对,并且记录大小
3、dm=min(d1,d2);
//预先排序的处理
4、设P1是S1中距垂直分割线l的距离在dm之内的所有点组成的集合;
P2是S2中距分割线l的距离在dm之内所有点组成的集合;
将P1和P2中点依其y坐标值排序;
并设X和Y是相应的已排好序的点列;
//1对6的扫描找最小值 所以最多是3 * n
5、通过扫描X以及对于X中每个点检查Y中与其距离在dm之内的所有点(最多6个)可以完成合并;
当X中的扫描指针逐次向上移动时,Y中的扫描指针可在宽为2dm的区间内移动;
设dl是按这种扫描方式找到的点对间的最小距离;
6、d=min(dm,dl);
return d;
}
核心过程就是第五步。
下面分析算法Cpair2的计算复杂性。设对于n个点的平面点集S ,算法耗时T(n)。算法的第1步和第5步用了𝑂(𝑛)时间。第3步和第6步用了常数时间。第2步用了2T(n/2)时间。若在每次执行第4步时进行排序,则在最坏情况下第4步要用𝑂(𝑛log𝑛)时间。这不符合我们 的要求。因此,在这里我们采用设计算法时常用的预排序技术,在使用分治法之前,预先将S中n个点依其y坐标值排好序,设排好序的点列为P 。在执行分治法的第4步时,只要对𝑃∗作一次线性扫描,即可抽取出我们所需要的排好序的点列X和Y。然后,在第5步中再对X作一次线性扫描,即可求得dl.因此,第4步和第5步的两遍扫描合在一起只要用0(n)时间。这样,经过预排序处理后算法Cpair2 所需的计算时间T(n)满足递归方程
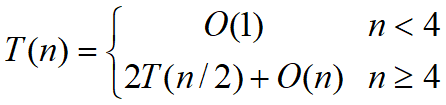
由此易知, T (n) = O(nlogn) 。预排序所需的计算时间显然为𝑂(𝑛log𝑛)。因此,整个算法所需的计算时间为𝑂(𝑛log𝑛),在渐近的意义下,此算法已是最优算法。
注意考试的时候要写上边界(n = 4)。
3.动态规划 #
基本概念和步骤 #
1、与分治法的异同 #
相同点:都是将求解问题分为若干个子问题
不同点:分治法所要求的子问题是独立的,而动态规划所求解的子问题往往不是独立的,重叠的子问题的多次运算可能会造成指数级的运算量。
2、动态规划的核心思想 #
**记表备查:**保存已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法。
3、解题步骤 #
1️⃣ 找出最优解的性质,并刻划其结构特征。
2️⃣ 递归地定义最优值。
3️⃣ 以自底向上的方式计算出最优值。
4️⃣ 根据计算最优值时得到的信息,构造最优解
4、基本要素 #
重叠子问题与最优子结构。
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。
要证明最优子结构的性质。
最优子结构的证明通常采用反证法,需要掌握。
全局的最优一定有局部的最优,局部的最优不一定会形成全局的最优,必要不充分条件
5、两种基本形态 #
动态规划(自底向上)与备忘录(memo)方法。
备忘录方法是动态规划方法的变形,都是记表备查,不同点在于备忘录方法是自顶向下的递归,而动态规划是自底向上的递归
一般来说,当一个问题的所有子问题都需要至少解一次时,用动态规划算法比用备忘录方法要好
具体问题设计 #
1.*矩阵连乘问题 #
给定n个矩阵𝐴1,𝐴2,…,𝐴𝑛,其中𝐴𝑖与𝐴𝑖+1是可乘的,i=1, 2,…, n-1。考察这n个矩阵的连乘积𝐴1𝐴2…𝐴𝑛。
由于矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。
完全加括号的矩阵连乘积可递归地定义为:
①单个矩阵是完全加括号的;
②矩阵连乘积A是完全加括号的,则A可表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号,即A=(BC)
设有四个矩阵A,B,C,D,可以有以下5种不同的加括号方式:
(A(B(CD))) (A((BC)D)) ((AB)(CD)) ((A(BC))D) (((AB)C)D)
每一种完全加括号方式对应于一种矩阵连乘积的计算次序,而矩阵连乘积的计算次序与其计算量有密切关系。矩阵A(p×q)和矩阵B(q×r)的乘积C=AB是一个p×r的矩阵,数乘次数为pqr
❓ 问题:
给定n个矩阵𝐴1,𝐴2,…,𝐴𝑛,其中𝐴𝑖与𝐴𝑖+1是可乘的,i=1, 2,…, n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
1)穷举法 #
计算次序相应需要的数乘次数,从中找出一种数乘次数最少的计算次序。
对于n个矩阵的连乘积,设其不同的计算次序为P(n)。由于每种加括号方式都可以分解为两个子矩阵的加括号问题:(A1…Ak)(Ak+1…An)可以得到关于P(n)的递推式如下:
这个数字太大,没有计算价值。
2)动态规划法 #
将矩阵连乘积AiAi+1…Aj简记为A[i:j] ,这里i≤j 。
考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开,i≤k<j,则其相应完全加括号方式为:
(AiAi+1…Ak) (Ak+1Ak+2…Aj)
计算量:A[i:k]的计算量加上A[k+1:j]的计算量,再加上A[i:k]和A[k+1:j]相乘的计算量。
1️⃣ 分析最优解的结构
特征:计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。
2️⃣ 建立递归关系
设计算A[i:j],1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n]。
设Ai的维数为𝑝𝑖−1×𝑝𝑖,则
当i=j时,𝐴[𝑖:𝑗]=𝐴𝑖,因此,m[i,i]=0,i=1,2,…,n
当i<j时,𝑚[𝑖:𝑗]=𝑚[𝑖,𝑘]+𝑚[𝑘+1,𝑗]+𝑝𝑖−1𝑝𝑘𝑝𝑗
可以递归地定义m[i,j]为:
必考问题。
k的位置只有j-i种可能
3️⃣ 计算最优值
对于1≤i≤j≤n不同的有序对(i,j)对应于不同的子问题。因此,不同子问题的个数最多只有
由此可见,在递归计算时,许多子问题被重复计算多次。这也是该问题可用动态规划算法求解的又一显著特征
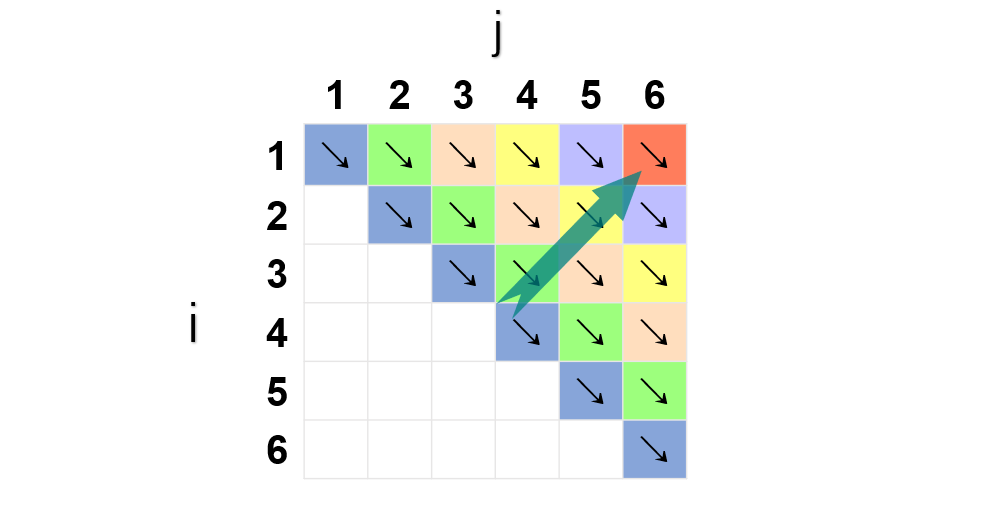
用动态规划算法解此问题,可依据其递归式以自底向上的方式进行计算。在计算过程中,保存已解决的子问题答案。每个子问题只计算一次,而在后面需要时只要简单查一下,从而避免大量的重复计算,最终得到多项式时间的算法。
代码如下:
public static void matrixChain(int[] p, int[][] dp, int[][] partitionIndex){
//有n个矩阵
int n = p.length - 1;
//初始化为0
for(int index = 0; index < n; ++index){
dp[index][index] = 0;
}
//控制矩阵链的长度
for(int len = 2; len <= n; ++len){
for(int i = 1; i <= n - len + 1; ++i){
//以第一个为基础
int j = i + len - 1;
dp[i][j] = dp[i + 1][j] + p[i + 1] * p[i] * p[j];
partitionIndex[i][j] = i;
for(int k = i + 1; k < j; ++k){
int value = dp[i][k] + p[i - 1] * p[k] * p[j] + dp[k + 1][j];
if(value < dp[i][j]){
dp[i][j] = value;
partitionIndex[i][j] = k;
}
}
}
}
}
算法MatrixChain的主要计算量取决于算法中对r,i和k的3重循环。循环体内的计算量为𝑂(1),而3重循环的总次数为𝑂(𝑛3)。因此算法的计算时间上界为𝑂(𝑛3)。算法所占用的空间显然为𝑂(𝑛2)。
traceback递归地来构造答案,那么完整可运行的代码如下:
package Dynamic;
public class demo01 {
public static void matrixChain(int[] p, int[][] dp, int[][] partitionIndex){
//有n个矩阵
int n = p.length - 1;
//初始化为0
for(int index = 0; index < n; ++index){
dp[index][index] = 0;
}
//控制矩阵链的长度
for(int len = 2; len <= n; ++len){
for(int i = 1; i <= n - len + 1; ++i){
//以第一个为基础
int j = i + len - 1;
dp[i][j] = dp[i + 1][j] + p[i + 1] * p[i] * p[j];
partitionIndex[i][j] = i;
for(int k = i + 1; k < j; ++k){
int value = dp[i][k] + p[i - 1] * p[k] * p[j] + dp[k + 1][j];
if(value < dp[i][j]){
dp[i][j] = value;
partitionIndex[i][j] = k;
}
}
}
}
}
public static void traceBack(int left, int right, int[][] partitionIndex){
if(left == right){
System.out.printf("A" + left);
}else{
System.out.print("(");
traceBack(left, partitionIndex[left][right], partitionIndex);
traceBack(partitionIndex[left][right] + 1, right, partitionIndex);
System.out.print(")");
}
}
public static void main(String[] args) {
int[] p = {30, 35, 15, 5, 10, 20, 25};
int n = 6;
int[][] m = new int[7][7];
int[][] s = new int[7][7];
matrixChain(p, m, s);
traceBack(1, 6, s);
System.out.println();
System.out.println(m[1][6]);
}
}
3)备忘录方法 #
memo (python:@cache)
备忘录方法的控制结构与直接递归方法的控制结构相同,区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看,避免了相同子问题的重复求解。
备忘录方法的递归方式是自顶向下的,而动态规划算法则是自底向上递归的。
用递归解决问题的期间把值记录起来。
以下是代码:
package Dynamic;
public class demo02 {
public static int lookUpChain(int left, int right, int[] p, int[][] m, int[][] partitionIndex){
if(m[left][right] > 0){
return m[left][right];
}
if(left == right){
return 0;
}
int min = lookUpChain(left, left, p, m, partitionIndex) + lookUpChain(left + 1, right, p, m, partitionIndex) + p[left - 1] * p[left] * p[right];
partitionIndex[left][right] = left;
for(int index = left + 1; index <= right; ++index){
int curr = lookUpChain(left, index, p, m, partitionIndex) + lookUpChain(index + 1, right, p, m, partitionIndex) + p[left - 1] * p[index] * p[right];
if(curr < min){
min = curr;
partitionIndex[left][right] = index;
}
}
m[left][right] = min;
return min;
}
}
2.凸多边形最优三角剖分 #
用多边形顶点的逆时针序列表示凸多边形,即P={v0,v1,…,vn-1}表示具有n条边的凸多边形。
若vi与vj是多边形上不相邻的2个顶点,则线段vivj称为多边形的一条弦。弦将多边形分割成2个多边形{vi,vi+1,…,vj}和{vj,vj+1,…,vi}。
多边形的三角剖分是将多边形分割成互不相交的三角形的弦的集合T。
注意:T中各弦互不相交,且集合T已达到最大;有n个顶点的凸多边形的三角剖分中,恰有n-3条弦和n-2个三角形。
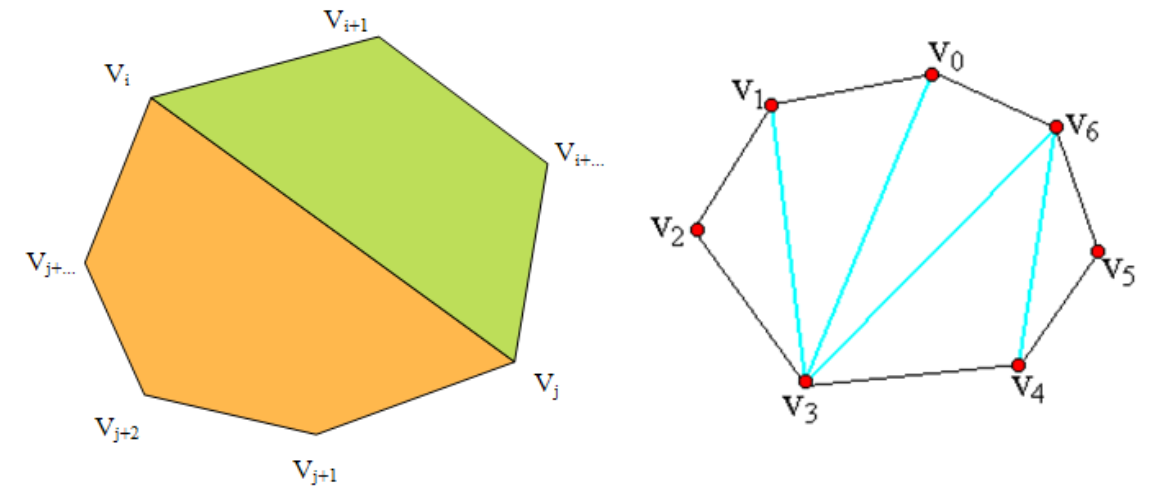
题目描述:给定凸多边形P,以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分,使得该三角剖分中诸三角形上权之和为最小。
① 三角剖分的结构 #
一个表达式的完全加括号方式相应于一棵完全二叉树,称为表达式的语法树。例如,完全加括号的矩阵连乘积((A1(A2A3))(A4(A5A6)))所相应的语法树如图 (a)所示。凸多边形{v0,v1,…vn-1}的三角剖分也可以用语法树表示。例如,图 (b)中凸多边形的三角剖分可用图 (a)所示的语法树表示。
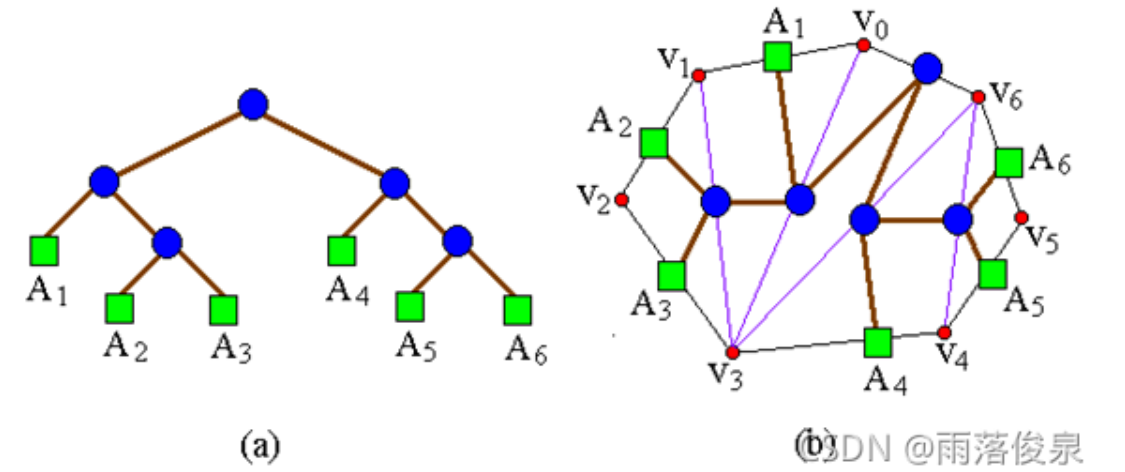
矩阵连乘积中的每个矩阵Ai对应于凸(n+1)边形中的一条边𝑣𝑖−1𝑣𝑖。三角剖分中的一条弦𝑣𝑖𝑣𝑗,i<j,对应于矩阵连乘积A[i+1:j]。
给定矩阵链𝐴1𝐴2𝐴3𝐴4𝐴5𝐴6,Ai的维数为𝑝𝑖−1×𝑝𝑖;定义凸多边形P={𝑣0,𝑣1,𝑣2,𝑣3,𝑣4,𝑣5,𝑣6},其三角形𝑣𝑖𝑣𝑗𝑣𝑘上的权函数值为𝑤(𝑣𝑖𝑣𝑗𝑣𝑘)=𝑝𝑖𝑝𝑗𝑝𝑘,依此定义,P的最优三角剖分所对应的语法树给出了矩阵链的最优完全加括号方式。
② 最优子结构性质 #
凸多边形的最优三角剖分问题有最优子结构性质。
证明的时候就要使用反证法。
事实上,若凸(n+1)边形P={v0,v1,…,vn-1}的最优三角剖分T包含三角形v0vkvn,1≤k≤n-1,则T的权为3个部分权的和:三角形v0vkvn的权,子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和。可以断言,由T所确定的这2个子多边形的三角剖分也是最优的。因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。
③ 最优三角形剖分的递归结构 #
注意定义的时候前面有一个-1,所以最优方案也是从1开始为t1n
定义𝑡[𝑖][𝑗],1≤i<j≤n为凸子多边形{vi-1, vi,…,vj}的最优三角剖分所对应的权函数值,即其最优值。为方便起见,设退化的多边形{vi-1,vi}具有权值0。据此定义,要计算的凸(n+1)边形P的最优权值为𝑡[1][𝑛]。
t [ i ] [ j ] 的值可以利用最优子结构性质递归地计算。当j-i≥1时,凸子多边形至少有3个顶点。由最优子结构性质,**$t[i][j]$**的值应为$t[i][k]$的值加上$t[k+1][j]$的值,再加上三角形$v_{i-1}v_kv_j$的权值,其中i≤k≤j-1。由于在计算时还不知道k的确切位置,而k的所有可能位置只有j-i个,因此可以在这j-i个位置中选出使值$t[i][j]$达到最小的位置。由此,$t[i][j]$可递归地定义为
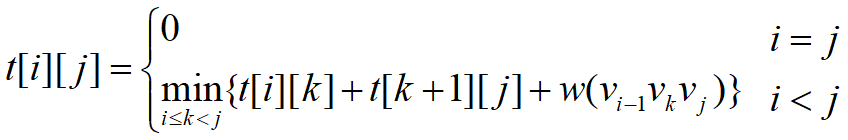
那么代码如下,和矩阵乘法是类似的处理方式:
package Dynamic;
public class demo03 {
public static int w(int a, int b, int c){
return a * b * c;
}
public static void minWeightTriangulation(int[] p, int[][] dp, int n, int[][] partitionIndex){
//initialize
for(int index = 1; index <= n; ++index){
dp[index][index] = 0;
}
for(int r = 2; r <= n; ++r){
for(int i = 1; i <= n - r + 1; ++i){
int j = i + r - 1;
int minValue = dp[i + 1][j] + w(i - 1, i, j);
partitionIndex[i][j] = i;
for(int k = i + 1; k < i + r - 1; ++k){
int currValue = dp[i][k] + w(i - 1, j, k) + dp[k + 1][j];
if(currValue < minValue){
minValue = currValue;
partitionIndex[i][j] = k;
}
}
}
}
}
}
3.多边形游戏 #
多边形游戏是一个单人玩的游戏,开始时有一个由n个顶点构成的多边形。每个顶点被赋予一个整数值,每条边被赋予一个运算符“+”或“*”。所有边依次用整数从1到n编号。
1️⃣ 游戏第1步,将一条边删除。
2️⃣ 随后n-1步按以下方式操作:
(1)选择一条边E以及由E连接着的2个顶点V1和V2;
(2)用一个新的顶点取代边E以及由E连接着的2个顶点V1和V2。将由顶点V1和V2的整数值通过边E上的运算得到的结果赋予新顶点。
3️⃣ 最后,所有边都被删除,游戏结束。游戏的得分就是所剩顶点上的整数值。
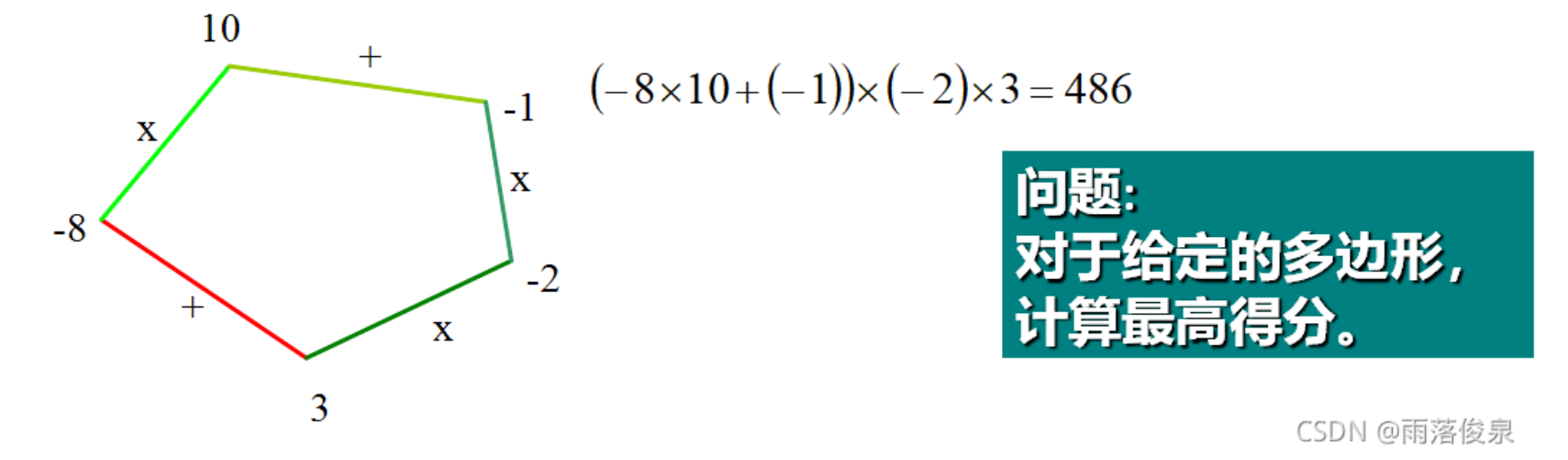

先只作证明,具体可以看书。
4.公园游艇问题(考试难度类似) #
题目描述:长江游艇俱乐部在长江上设置了n 个游艇出租站{1,2,…,n}。游客可在这些游艇出租站租用游艇,并在下游的任何一个游艇出租站归还游艇。游艇出租站 i 到游艇出租站 j 之间的租金为r(i,j),1≤i<j≤n。试设计一个算法,计算出从游艇出租站 1 到游艇出租站 n 所需的最少租金。
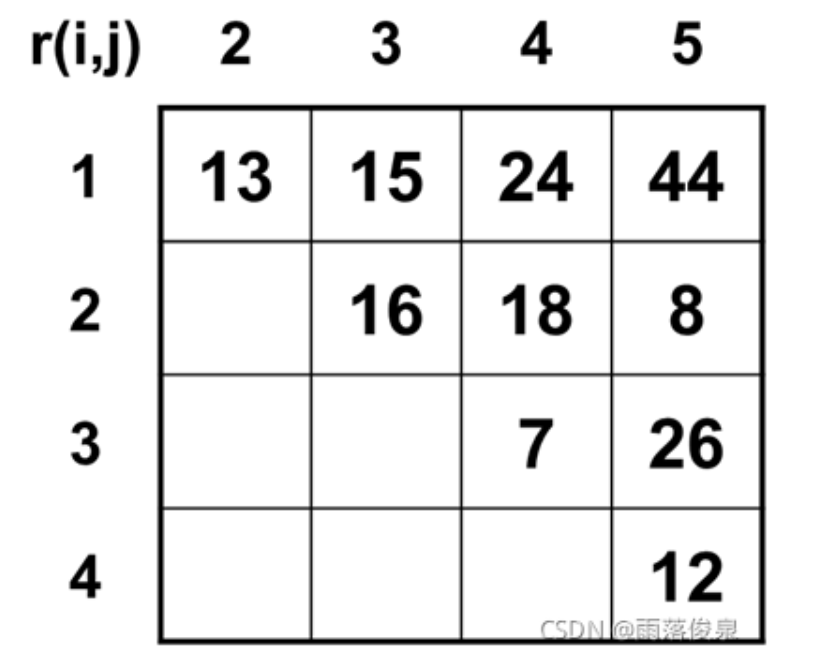
思考一下,还是和矩阵连乘的问题是类似的。
1️⃣ 最优解结构
r(i,j)表示游艇出租站i直接到j之间的租金,m(i,j)表示从出租站i出发,到达第j站需要的租金 例如m(1,3)就表示从第1站出发,到达第3站所需的租金,而m(1,3)可以有多种租用方案,例如可以1-2.2-3与1-3。
假设在第k站换游艇( i ≤ k ≤ j ) ,则有m(i,j)=m(i,k)+m(k,j),其中m(i,j)的最优解包括m(i,k)与m(k,j)的最优解。
2️⃣ 建立递归关系
由以上分析可知,显然有:
3️⃣ 计算最优值
void cent(int[][] m, int n, int[][] s) {
for (int i = 1; i <=n ; i++) {
m[i][i]=0;
}
for (int r = 2; r <= n; r++)
for (int i = 1; i <= n - r + 1; i++) {
int j = i + r - 1;
s[i][j] = i;
for (int k = i; k <= j; k++) {
int temp = m[i][k] + m[k][j];
if (temp < m[i][j]) {
m[i][j] = temp;
s[i][j] = k;//在第k站下
}
}
}
}
构造最优解:
void traceBack(int i, int j, int[][] s) {
if (i == j) {
System.out.print(i);
return;
}
System.out.print("[");
traceBack(i, s[i][j], s);
traceBack(s[i][j] + 1, j, s);
System.out.print("]");
}
5.最大子段和 #
和最大的一个连续子数组。
LeetCode:https://leetcode.cn/problems/maximum-subarray/description/
题目描述:给定由n个整数(可能为负整数)组成的序列a1,a2,…,an,求该序列子段和的最大值。当所有整数均为负整数时定义其最大子段和为0。依此定义,所求的最优值为:
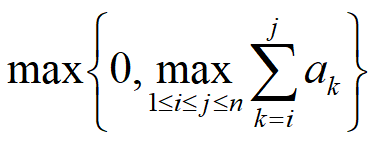
例,序列{-2,11,-4,13,-5,-2}的最大子段和为20。
做法:定义状态 f[i] 表示以 a[i] 结尾的最大子数组和,不和 i 左边拼起来就是 f[i]=a[i],和 i 左边拼起来就是 f[i]=f[i−1]+a[i],取最大值就得到了状态转移方程 f[i]=max(f[i−1],0)+a[i],答案为 max(f)。这个做法也叫做 Kadane 算法。
由b[j]的定义易知,当b[j-1]>0时,b[j]=b[j-1]+a[j],否则b[j]=a[j],故
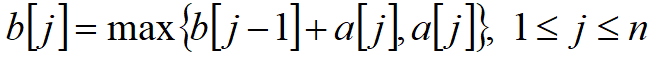
代码如下:
class Solution {
public int maxSubArray(int[] nums) {
int ans = nums[0];
int n = nums.length;
int[] dp = new int[n];
dp[0] = nums[0];
for(int index = 1; index < n; ++index){
if(dp[index - 1] < 0){
dp[index] = nums[index];
}else{
dp[index] = dp[index - 1] + nums[index];
}
ans = Math.max(ans, dp[index]);
}
return ans;
}
}
最大子段和问题与动态规划算法的推广 #
1、最大子矩阵和问题 #
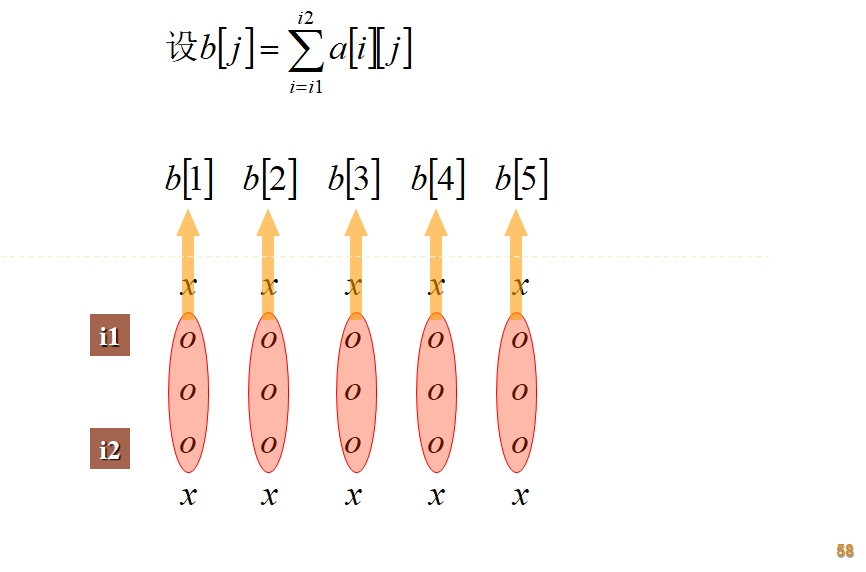
给定一个m行n列的整数矩阵A,试求矩阵A的一个子矩阵,使其各元素之和为最大。
把每两行之间的数字相加起来,使之成为一个一维的数组,接着用上面的方法来处理即可,这个问题比较简单。
/**
* 最大子矩阵和
* @param m
* @param n
* @param a
* @return
*/
public static int MaxSum2(int m,int n,int[][]a){
int sum=0;
int[]b=new int[n];
for(int i=0;i<m;i++){ //从第i行
for(int k=0;k<n;k++) //初始化数组b
b[k]=0;
for(int j=i;j<m;j++){ //到第j行
for(int k=0;k<n;k++)
b[k]+=a[j][k];//按列取值
int max=solveByDP(b);
if(max>sum)
sum=max;
}
}
return sum;
}
2.*最大M子段和问题 #
定由n个整数(可能为负数)组成的序列{a1,a2,…,an},以及一个正整数m,要求确定序列{a1,a2,…,an}的m个不相交子段,使这m个子段的总和达到最大。
设b(i,j)表示数组a的前j项中i个子段和的最大值,且第i个子段含a[j](1≤i ≤ m,i ≤j ≤n),则计算b(i,j)的递归式为
初始时
b(0,j)=0, (1≤j ≤n)
b(i,0)=0, (1≤i ≤m)
int MaxSum(int m,int n,int *a)
{
if(n<m||m<1)
return 0;
int **b=new int *[m+1]; //定义二维数组b
for(int i=0; i<=m; i++)
b[i]=new int[n+1];
for(int i=0; i<=m; i++) //初始值
b[i][0]=0;
for(int j=1; j<=n; j++)
b[0][j]=0;
for(int i=1; i<=m; i++) //1≤i ≤m
for(int j=i; j<n-m+i; j++) //j≥i, t<j
if(j>i)
{
b[i][j]=b[i][j-1]+a[j];
for(int k=i-1; k<j; k++) //i-1≤t<j
if(b[i][j]<b[i-1][k]+a[j])
b[i][j]=b[i-1][k]+a[j];
}
else //j=i, 每个数都是一个子段
b[i][j]=b[i-1][j-1]+a[j];
int sum=0;
for(int j=m; j<=n; j++)
if(sum<b[m][j])
sum=b[m][j];
return sum;
}
6.*图像压缩问题(没看懂) #
我没看懂在干嘛,先放着吧。
计算机中常用像素点灰度值序列{𝑝1,𝑝2,…,𝑝𝑛}表示图像,𝑝𝑖表示像素点i的灰度值。灰度值的范围常为0~255,需要用8位来表示。
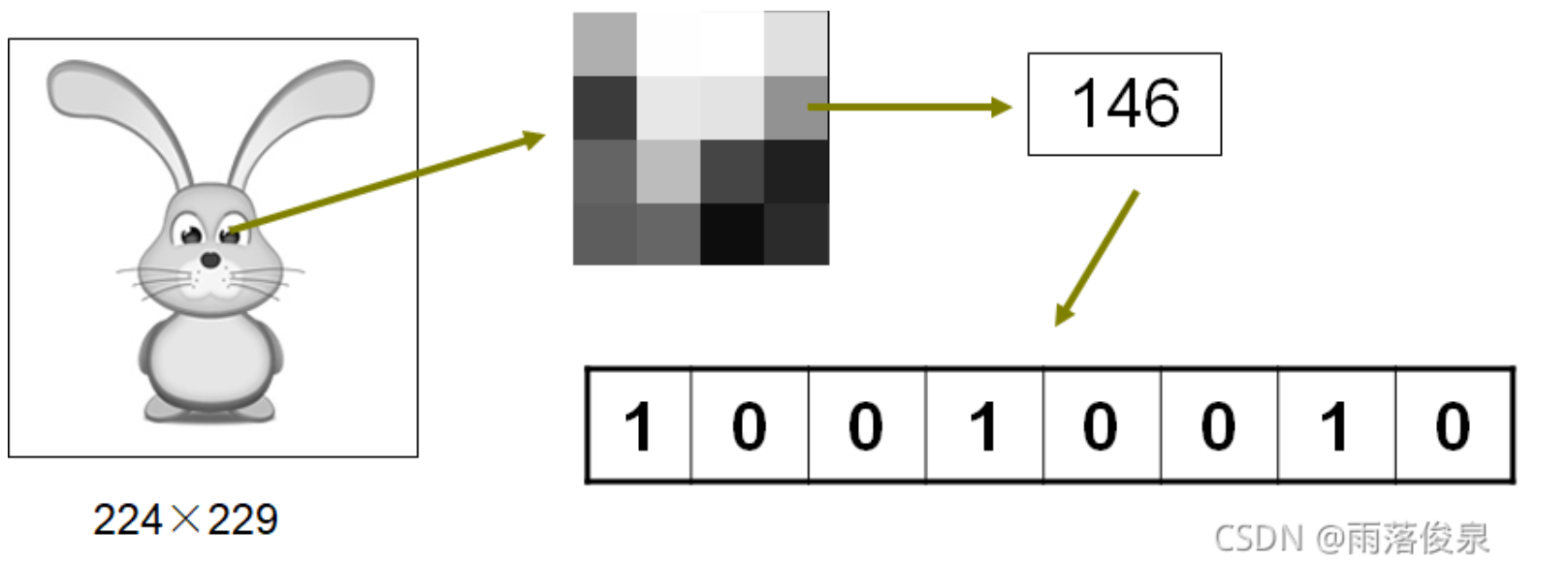
图像的变位压缩存储格式将所给的像素点序列{𝑝1,𝑝2,…,𝑝𝑛}分割成m个连续段{𝑆1,𝑆2,…,𝑆𝑚}。第i个像素段Si中有l[i]个像素,且该段中每个像素都只用b[i]位表示。需用3位表示b[i],如果限制1≤l[i]≤255,则需要用8位表示l[i],因此第i个像素段所需的存储空间为l[i]*b[i]+11。——即一段中最多有255个像素,用8位二进制表示
整个像素序列的存储空间为
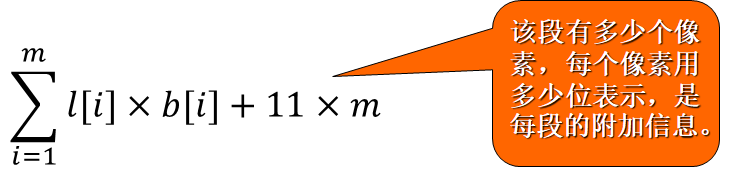
问题描述:确定像素序列{p1,p2,…,pn}的一个最优分段,使得依此分段所需的存储空间最小。其中0≤pi ≤255,1 ≤i ≤n,每个分段的长度不超过255位。
1️⃣ 最优子结构 #
设l[i],b[i],1≤i ≤m是{𝑝1,𝑝2,…,𝑝𝑛}的最优分段。显而易见,l[1],b[1]是{𝑝1,𝑝2,…,𝑝𝑙[1]}的最优分段,且l[i],b[i], 2≤i ≤m是
{𝑝𝑙[1]+1,…,𝑝𝑛}的最优分段。即图象压缩问题满足最优子结构性质。
2️⃣ 递归计算最优值 #
设s[i],1≤i≤n,是像素序列{𝑝1,𝑝2,…,𝑝𝑖}的最优分段所需的存储位数。由最优子结构性质易知:
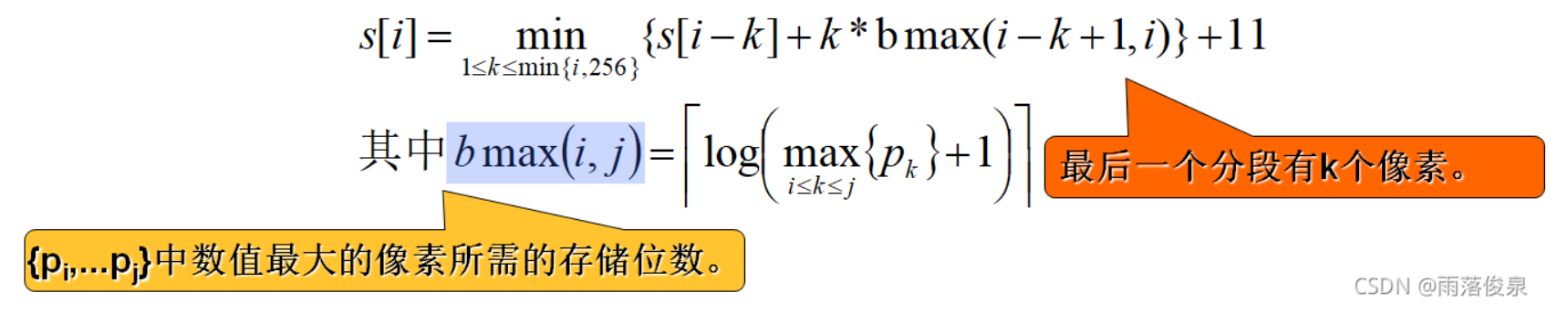
举例:

3️⃣ 构造最优解 #
算法用l[i],b[i]记录了最优分段所需的信息。
最优分段的最后一段的段长和像素位数分别存储于l[n]和b[n]中,其前一段的段长度和像素位数存储于l[n-l[n]]和b[n-l[n]]中。依此类推,可在O(n)时间内构造出相应的最优解
/**
* 计算十进制数i所需的二进制位数
*
* @param i
* @return
*/
static int length(int i) {
int k = 1;
i = i / 2;
while (i > 0) {
k++;
i = i / 2;
}
return k;
}
/**
* @param n
* @param l [p1:pi]的最优分段中最后1个分段的像素个数
* @param p p[p1:pn],像素点灰度值序列
* @param s 像素序列[p1:pi]的最优分段所需的存储位数
* @param b 像素p[i]所需的存储位数
*/
public static void Compress(int n, int[] p, int[] s, int[] l, int[] b) {
int Lmax = 255;//每个分段的长度不超过255位
int header = 11;//分段段头所需的位数,表示一个段的附加信息
s[0] = 0;
for (int i = 1; i <= n; i++) //[p1:pi]
{
b[i] = length(p[i]);
int bmax = b[i];
s[i] = s[i - 1] + bmax; //k=1
l[i] = 1;
for (int j = 2; j <= i && j <= Lmax; j++) //最后的1个分段中有j个像素
{
if (bmax < b[i - j + 1])
bmax = b[i - j + 1];//这一段中的最大位数
if (s[i] > s[i - j] + j * bmax) {//找到更好的分段
s[i] = s[i - j] + j * bmax;
l[i] = j;
}
}
s[i] += header;//加上额外开销
}
}
public static int Traceback(int n, int i, int[] s, int[] l) {
if (n == 0)
return i;
i = Traceback(n - l[n], i, s, l);
s[i++] = n - l[n];// 重新为s[]数组赋值,用来存储分段位置
return i;
}
static void Output(int s[], int l[], int b[], int n) {
System.out.println("The optimal value is " + s[n]);
int m = 0;
m=Traceback(n, m, s, l); //m:分段数
s[m] = n; //m个分段像素的累积和,Traceback算到m-1个
System.out.println("Decompose into " + m + " segments");
for (int j = 1; j <= m; j++) {
l[j] = l[s[j]]; //计算第j个分段像素个数: l[j]
b[j] = b[s[j]]; //计算第j个分段所需的存储位数: b[j]
}
for (int j = 1; j <= m; j++)
System.out.println(l[j] + " " + b[j]);
}
public static void main(String[] args) {
int p[] = {0,10,12,15,255,2,1};//第一位不算
int N=p.length;
int s[] = new int[N];
int l[] = new int[N];
int b[] = new int[N];
Compress(N-1, p, s, l, b);
Output(s, l, b, N-1);
}
}
7.*最长公共子序列 #
LeetCode:https://leetcode.cn/problems/longest-common-subsequence/description/
若给定序列𝑋=𝑥1,𝑥2,…,𝑥𝑚,则另一序列𝑍=𝑧1,𝑧2,…,𝑧𝑘,是X的子序列是指存在一个严格递增下标序列𝑖1,𝑖2,…,𝑖𝑘使得对于所有j=1,2,…,k有:𝑧𝑗=𝑥𝑖𝑗。例如,序列Z={B, C, D, B}是序列X={A, B, C , B, D, A, B}的子序列,相应的递增下标序列为{2, 3, 5, 7}。给定2个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。例:X={A,B,C,B,D,A,B},Y={B,D,C,A,B,A},则序列{B,C,A}是X和Y的一个公共子序列。
1)最长公共子序列的结构 #
设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则
⑴若xm=yn,则zk=xm=yn,且Zk-1是Xm-1和Yn-1的最长公共子序列。
⑵若xm≠yn且zk≠xm,则Z是Xm-1和Y的最长公共子序列。
⑶若xm≠yn且zk≠yn,则Z是X和Yn-1的最长公共子序列。
由此可见,2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列。因此,最长公共子序列问题具有最优子结构性质。
2)子问题的递归结构 #
由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。用𝑐[𝑖][𝑗]记录序列的最长公共子序列的长度。其中,
X i = x 1 , x 2 , … , x i ; Y j = y 1 , y 2 , … , y j 。当i=0或j=0时,空序列是Xi和Yj的最长公共子序列。故此时𝐶[𝑖][𝑗]=0。其它情况下,由最优子结构性质可建立递归关系如下:
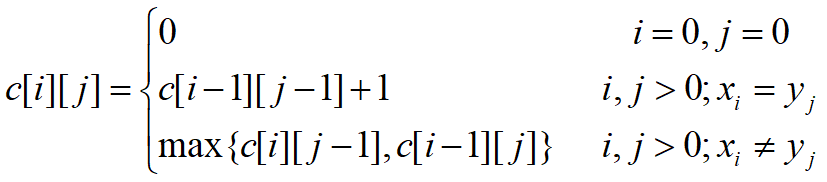
3)计算最优值 #
由于在所考虑的子问题空间中,总共有θ(mn)个不同的子问题,因此,用动态规划算法自底向上地计算最优值能提高算法的效率。
输入:x,y (序列数组)
输出:
c [ i ] [ j ] ,存储x[1:i]和y[1:j]的最长公共子序列的长度;
b [ i ] [ j ] ,记录上面𝑐[𝑖][𝑗]的值是由哪个子问题的解得到的。
/**
* 计算最长公共子序列
* @param x 序列数组
* @param y 序列数组
* @param c 存储x[1:i]和y[1:j]的最长公共子序列的长度
* @param b 记录上面c[i][j]的值是由哪个子问题的解得到的
*/
public static void LCSLength(char[] x, char[] y, int[][] c, int[][] b) {
int m = x.length-1;
int n = y.length-1;
for (int i = 1; i <= m; i++) {
c[i][0] = 0;
}
for (int i = 1; i <= n; i++) {
c[0][i] = 0;
}//第一个条件
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (x[i] == y[j]) {
c[i][j] = c[i - 1][j - 1] + 1;
b[i][j] = 1;
//表示Xi和Yi的最长公共子序列是由Xi-1和Yi-1的最长公共子序列在尾部加上xi所得到的。
} else if (c[i - 1][j] >= c[i][j - 1]) {
c[i][j] = c[i - 1][j];
b[i][j] = 2;
//表示Xi和Yi的最长公共子序列与Xi-1和Yi的最长公共子序列相同
} else {
c[i][j] = c[i][j - 1];
b[i][j] = 3;
//表示Xi和Yi的最长公共子序列与Xi和Yj-1的最长公共子序列相同
}
}
}
}
算法耗时O(mn)
4)构造最长公共子序列 #
从𝑏[𝑚][𝑛] 开始,依其值在数组b中搜索。
b [ i ] [ j ] 的值为:
1,表示Xi和Yi的最长公共子序列是由Xi-1和Yi-1的最长公共子序列在尾部加上xi所得到的。
2,表示Xi和Yi的最长公共子序列与Xi-1和Yi的最长公共子序列相同。
3, 表示Xi和Yi的最长公共子序列与Xi和Yi-1的最长公共子序列相同。
public static void LCS(int m, int n, char[] x, int[][] b) {
if (m == 0 || n == 0) {
return;
}
if (b[m][n] == 1) {
LCS(m - 1, n - 1, x, b);
System.out.print(x[m]);
} else if (b[m][n] == 2) {
LCS(m - 1, n, x, b);
} else {
LCS(m, n - 1, x, b);
}
}
5)算法的改进 #
在算法lcsLength和lcs中,可进一步将数组b省去。事实上,数组元素𝑐[𝑖][𝑗]的值仅由,和𝑐[𝑖−1][𝑗−1],𝑐[𝑖−1][𝑗]和𝑐[𝑖][𝑗−1]这3个数组元素的值所确定。对于给定的数组元素𝑐[𝑖][𝑗],可以不借助于数组b而仅借助于c本身在O(1)时间内确定𝑐[𝑖][𝑗]的值是由,和𝑐[𝑖−1][𝑗−1],𝑐[𝑖−1][𝑗]和𝑐[𝑖][𝑗−1]中哪一个值所确定的。
如果只需要计算最长公共子序列的长度,则算法的空间需求可大大减少。事实上,在计算𝑐[𝑖][𝑗]时,只用到数组c的第i行和第i-1行。因此,用2行的数组空间就可以计算出最长公共子序列的长度。进一步的分析还可将空间需求减至O(min(m,n))。
8.电路布线问题 #
LeetCode类似问题:https://leetcode.cn/problems/uncrossed-lines/description/
LCS的变种。
在一块电路板的上、下2端分别有n个接线柱。根据电路设计,要求用导线(i,π(i))将上端接线柱与下端接线柱相连,其中π(i)是{1,2,…,n}的一个排列。导线(i,π(i))称为该电路板上的第i条连线。对于任何1≤i<j≤n,第i条连线和第j条连线相交的充分且必要的条件是π(i)>π(j)。
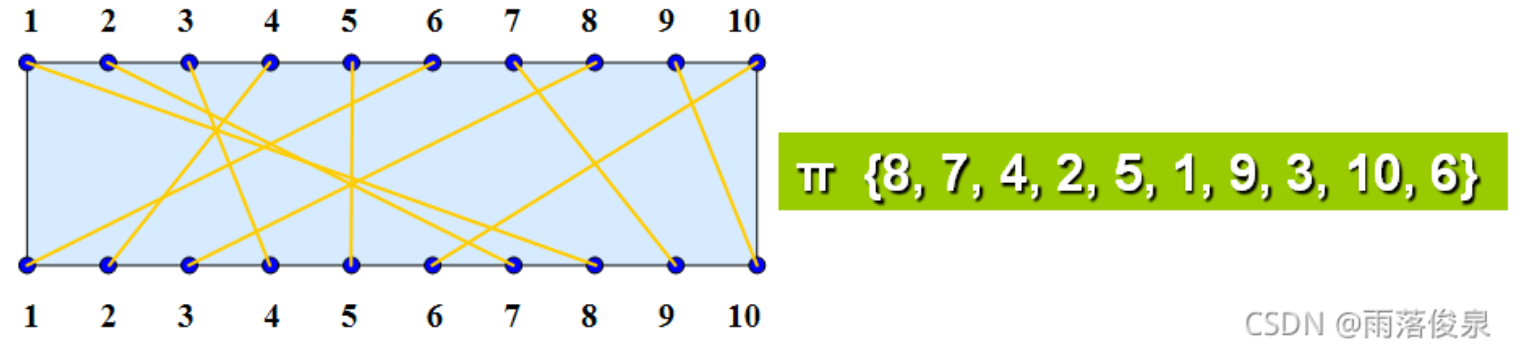
电路布线问题要确定将哪些连线安排在第一层上,使得该层上有尽可能多的连线。换句话说,该问题要求确定导线集Nets={(i,π(i)),1≤i≤n}的最大不相交子集。
最优子结构性质 #
看清楚这里N(i,j)的实际含义。t <= i……

考试前再看一下,比较有意思。
代码:
void MNS(int C[],int n,int **size){
//C[i],即π[i]
//size[i][j],N(i,j)的最大不相交子集中连线的数目
for(int j=0; j<C[1]; j++) //i=1,j<π(1)
size[1][j]=0;
for(int j=C[1]; j<=n; j++) //i=1,j>=π(1)
size[1][j]=1;
for(int i=2; i<n; i++) //1<i<n
{
for(int j=0; j<C[i]; j++) //j<π(i)
size[i][j]=size[i-1][j];
for(int j=C[i]; j<=n; j++) //j>=π(i)
size[i][j]=max(size[i-1][j],size[i-1][C[i]-1]+1);
}
size[n][n]=max(size[n-1][n],size[n-1][C[n]-1]+1); //i=n,j=n
}
void Traceback(int C[],int **size,int n,int Net[],int &m)
{
//Net[0:m-1]存储MNS(n,n)中的m条连线
int j=n;
m=0;
for(int i=n; i>1; i--)
if(size[i][j]!=size[i-1][j]) //第i条连线∈MNS(n,n)
{
Net[m++]=i;
j=C[i]-1; //π[i]
}
if(j>=C[1]) //i=1
Net[m++]=1;
}
9.01背包问题(重要) #
可以看代码随想录,我不知道为什么课本能写的这么逆天。
但是要理解书上的关于跳跃点的问题。
重要:背下来
给定n种物品和一背包。物品i的重量是𝑤𝑖,其价值为𝑣𝑖,背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
0-1背包问题是一个特殊的整数规划问题

1️⃣ 最优子结构性质(证明题) #
注意证明的方法和思想。
设(y1,y2,…,yn)是所给问题的一个最优解,则(y2,y3,…,yn)是下面相应子问题的的一个最优解:
若不然,设(z2,z3,…,zn)是上述子问题的一个最优解。
这说明(y1,z2,…,zn)是所给问题的一个更优解,从而与(y1,y2,…,yn)是所给问题的最优解相矛盾。
在这里反推矛盾,书上这里还写错了,纯垃圾书!
2️⃣ 递归关系 #
设所给0-1背包问题的子问题的最优值为m(i,j),即m(i,j)是背包容量为j,可选择物品为i,i+1,…,n时0-1背包问题的最优值。
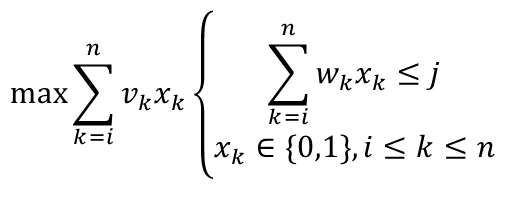
由0-1背包问题的最优子结构性质,可以建立计算m(i,j)的递归式如下。
3️⃣ 算法描述 #
public class KnapsackProblem {
//0-1背包问题
/**
*
* @param v v[1:n],物品i的价值
* @param w w[1:n],物品i的重量
* @param c 背包容量
* @param n
* @param m m[i][j],背包容量为j,可选物品为[i:n]时,0-1背包问题的最优值
*/
public static void Knapsack(int[]v,int[]w,int c,int n,int[][]m){
int jMax = Math.min(w[n]-1,c);
for (int j = 0; j <=jMax; j++) {
m[n][j]=0;//j<=c&&j<w[n],物品n无法放入背包
}
for (int j = w[n]; j <=c; j++) {
m[n][j]=v[n];//w[n]<=j<=c,物品n可以放入背包
}//画边界,从后往前看
for (int i = n-1; i >1 ; i--) {
jMax = Math.min(w[i]-1,c);
for (int j = 0; j <=jMax; j++) {
m[i][j]=m[i+1][j];//物品i无法放入背包
}
for (int j = w[i]; j <=c ; j++) {//物品i可放入背包
m[i][j]=Math.max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
}
}
m[1][c]=m[2][c];
if (c>=w[1]){
m[1][c]=Math.max(m[1][c],m[2][c-w[1]]+v[1]);
}
}
/**
* 求解
* @param m
* @param w
* @param c
* @param n
* @param x 具体的解
*/
public static void TraceBack(int[][]m, int[]w,int c,int n,int[]x){
for(int i=1;i<n;i++)
if(m[i][c]==m[i+1][c])
x[i]=0;
else
{
x[i]=1;
c-=w[i];
}
x[n]=(m[n][c]>0)?1:0;
}
public static void main(String[] args) {
int[]v={0,1,13,8,4,5,6,7};
int[]w={0,2,3,1,4,1,5,1};
int c = 10;
int n = v.length;
int[] x = new int[n];
int[][]m=new int[n][c+1];
Knapsack(v,w,c,n-1,m);
TraceBack(m,w,c,n-1,x);
for (int i = 1; i < n; i++) {
System.out.println(x[i]+" ");
}
}
}
一维的优化问题:
以下从代码随想录的网站上复制的
一维dp数组(滚动数组) #
对于背包问题其实状态都是可以压缩的。
在使用二维数组的时候,递推公式:dpi = max(dpi - 1, dpi - 1] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dpi = max(dpi, dpi] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。
这就是滚动数组的由来,需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
读到这里估计大家都忘了 dpi里的i和j表达的是什么了,i是物品,j是背包容量。
dpi 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
一定要时刻记住这里i和j的含义,要不然很容易看懵了。
动规五部曲分析如下:
- 确定dp数组的定义
关于dp数组的定义,我在 01背包理论基础
(opens new window) 有详细讲解
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
- 一维dp数组的递推公式
二维dp数组的递推公式为: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
公式是怎么来的 在这里 01背包理论基础
(opens new window) 有详细讲解。
一维dp数组,其实就上上一层 dp[i-1] 这一层 拷贝的 dp[i]来。
所以在 上面递推公式的基础上,去掉i这个维度就好。
递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
以下为分析:
dp[j]为 容量为j的背包所背的最大价值。
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 [j - 物品i重量] 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dpi-1,即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
所以递归公式为:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
可以看出相对于二维dp数组的写法,就是把dpi中i的维度去掉了。
- 一维dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
- 一维dp数组遍历顺序
代码如下:
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
这里大家发现和二维dp的写法中,遍历背包的顺序是不一样的!
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
为什么呢?
倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
举一个例子:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
为什么倒序遍历,就可以保证物品只放入一次呢?
倒序就是先算dp[2]
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0)
dp[1] = dp[1 - weight[0]] + value[0] = 15
所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
那么问题又来了,为什么二维dp数组遍历的时候不用倒序呢?
因为对于二维dp,dpi都是通过上一层即dpi - 1计算而来,本层的dpi并不会被覆盖!
(如何这里读不懂,大家就要动手试一试了,空想还是不靠谱的,实践出真知!)
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!
因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经讲了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的!,这一点大家一定要注意。
10.最优二叉搜索树 #
TODO:
4.贪心算法 #
由局部最优推理全局最优,但是结果不一定正确,数学上的证明才能说明最好。
一般来说简单的贪心都会先考虑排序问题。
1.活动安排问题 #
活动安排问题:要求高效地安排一系列争用某一公共资源的活动。
| 活动序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 起始时间 | 1 | 3 | 0 | 5 | 3 | 5 | 6 | 8 | 8 | 2 | 12 |
| 结束时间 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
1、问题定义 #
设有n个活动的集合E={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。(临界资源)
每个活动i都有一个要求使用该资源的起始时间𝑠𝑖和一个结束时间𝑓𝑖,且𝑠𝑖<𝑓𝑖 。
如果选择了活动i,则它在半开时间区间[𝑠𝑖,𝑓𝑖)内占用资源。若区间与[𝑠𝑖,𝑓𝑖)区间[𝑠𝑗,𝑓𝑗)不相交,则称活动i与活动j是相容的。即,当𝑠𝑖≥𝑓𝑗或𝑠𝑗≥𝑓𝑖时,活动i与活动j相容,
问题就是选择一个由互相兼容的活动组成的最大集合
2、实现代码 #
template<class Type>
void GreedySelector(int n, Type s[], Type f[], bool A[])
{
//各活动的起始时间和结束时间存储在数组s和f中
//且按结束时间的非递减排序:f1≤f2≤…≤fn排列。
A[1]=true; //用集合A存储所选择的活动
int j=1;
for(int i=2; i<=n; i++) {
//将与j相容的具有最早完成时间的相容活动加入集合A
if(s[i]>=f[j]) A[i]=true; j=i;
else A[i]=false;
}
}
3、算法分析 #
设集合a包含已被选择的活动, 初始时为空。所有待选择的活动按结束时间的非递减顺序排列:𝑓1≤𝑓2≤…𝑓𝑛
变量j指出最近加入a的活动序号。由于按结束时间非递减顺序来考虑各项活动的,所以𝑓𝑗总是a中所有活动的最大结束时间
由于输入活动是以完成时间的非递减排列,所选择的下一个活动总是可被合法调度的活动中具有最早结束时间的那个,所以算法是一个**“贪心的”选择**,即使得使剩余的可安排时间段极大化,以便安排尽可能多的相容活动。
4、复杂性分析 #
算法GreedySelector的效率极高。当输入的活动已按结束时间的非减序排列,算法只需O(n)的时间就可安排n个活动,使最多的活动能相容地使用公共资源。 如果所给出的活动未按非减序排列,可以用O(nlogn)的时间重排。
5、贪心选择性质和最优子结构性质证明 #
还是注意贪心的证明的方法。
设集合E={1,2,…,n}为所给的活动集合。由于E中活动按结束时间的非减序排列,故活动1有最早完成时间。
证明I:活动安排问题有一个最优解以贪心选择开始,即该最优解中包含活动1。
证明II:对集合E中所有与活动1相容的活动进行活动安排求得最优解的子问题。
即需证明:若A是原问题的最优解,则A’=A-{1}是活动安排问题E’={i∈E:si≥f1}的最优解。
非常浅显的证明,考试前看一下。
如果能找到*E*’的一个最优解*B*’,它包含比*A*’更多的活动,则将活动1加入到*B*’中将产生*E*的一个解*B*,它包含比*A*更多的活动。这与*A*的最优性矛盾。
结论:每一步所做的贪心选择问题都将问题简化为一个更小的与原问题具有相同形式的子问题。
2.01背包问题 #
与0-1背包问题类似,所不同的是在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包。 此问题的形式化描述为,给定𝑐>0,𝑤𝑖>0,𝑣𝑖>0,1≤𝑖≤𝑛,要求找出一个n元0-1向量(𝑥1,𝑥2,..,𝑥𝑛),其中0≤𝑥𝑖≤1,1≤𝑖≤𝑛 ,使得对𝑤𝑖𝑥𝑖求和小于等于c ,并且对𝑣𝑖𝑥𝑖求和达到最大。
对于0-1背包问题,贪心选择之所以不能得到最优解是因为,在这种情况下,无法保证最终能把背包装满,部分闲置的背包空间会使每千克背包空间的价值降低。
1、题目描述 #
有3种物品,背包的容量为50千克。物品1重10千克,价值60元;物品2重20千克,价值100元;物品3重30千克,价值120元。用贪心算法求背包问题。
2、基本步骤 #
首先计算每种物品单位重量的价值𝑣𝑖/𝑤𝑖;
还是根据这个单位重量进行一个排序。
然后,依贪心选择策略,将尽可能多的单位重量价值最高的物品装入背包。
若将这种物品全部装入背包后,背包内的物品总重量未超过c,则选择单位重量价值次高的物品并尽可能多地装入背包。依此策略一直地进行下去,直到背包装满为止。
3、贪心策略 #
贪心策略:物品1,6元/千克;物品2,5元/千克;物品3,4元/千克。
4、算法描述 #
该算法前提:所有物品在集合中按其单位重量的价值从小到大排列。
void Knapsack(int n, float M, float v[], float w[], float x[]) {
sort(n, v, w);//按照单位价值从小到大排列
int i;
for (i = 1; i <= n; i++) x[i] = 0;
float c = M;
for (i = 1; i <= n; i++) {
if (w[i] > c) break;
x[i] = 1;
c -= w[i];
}
if (i <= n) x[i] = c / w[i];//按比例放
}
算法Knapspack的主要计算时间在于将各种物品按其单位重量的价值从小到大排序,算法的时间复杂度O(nlogn) 。
3.HaffMan编码 #
7分简答题
学过数据结构就比较简单。
哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%~90%之间。
哈夫曼编码算法是用字符在文件中出现的频率表来建立一个用0,1串表示各字符的最优表示方式。
编码目标:给出现频率高的字符较短的编码,出现频率较低的字符以较长的编码,可以大大缩短总码长。
1、前缀码(考点) #
定义:对每一个字符规定一个0,1串作为其代码,并要求任一字符的代码都不是其他字符代码的前缀。这种编码称为前缀码。
编码的前缀性质可以使译码方法非常简单。由于任一字符的代码都不是其他字符代码的前缀,从编码文件中不断取出代表某一字符的前缀码,转换为原字符,即可逐个译出文件中的所有字符。
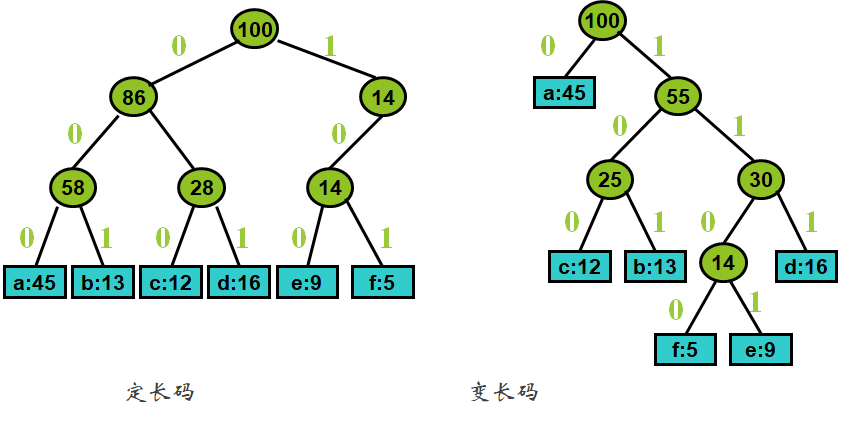
规定一下,小的数字放在二叉树的左子结点,大的数字放在二叉树的右边子结点,左边是0,右边是1。
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| 频率 | 45 | 13 | 12 | 16 | 9 | 5 |
| 定长码 | 000 | 001 | 010 | 011 | 100 | 101 |
| 变长码 | 0 | 101 | 100 | 111 | 1101 | 1100 |
给定序列:001011101,可以唯一的分解为0,0,101,1101,编译为aabe
2、问题分 #
译码过程需要方便地取出编码的前缀,因此需要一个表示前缀码的合适的数据结构。
用二叉树作为前缀编码的数据结构。在表示前缀码的二叉树中,树叶代表给定的字符,并将每个字符的前缀码看作是从树根到代表该字符的树叶的一条道路。代码中每一位的0或1分别作为指示某结点到其左儿子或右儿子的“路标”。
3、前缀码的二叉树表示 #
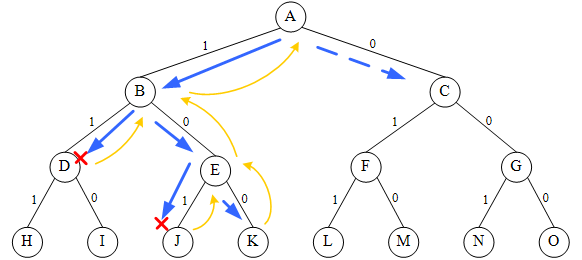
4、构造哈夫曼编码(考点) #
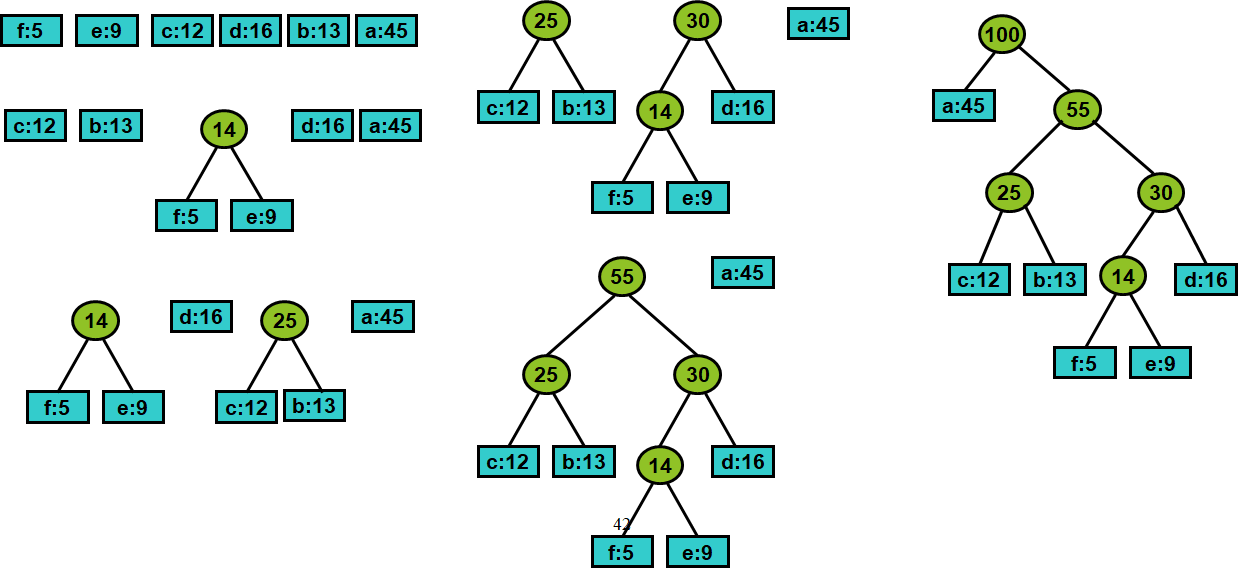
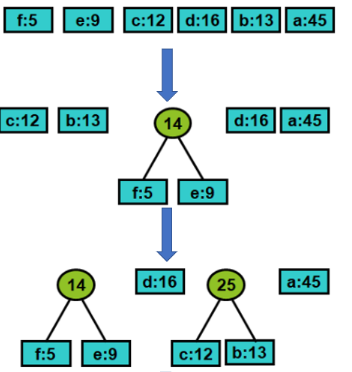
哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。
编码字符集中每一字符c的频率是f(c)。以f为键值的优先队列Q用以在作贪心选择时有效地确定算法当前要合并的两棵具有最小频率的树。一旦两棵具有最小频率的树合并后,产生一棵新的树,其频率为合并的两棵树的频率之和,并将新树插入优先队列Q中,再进行新的合并。
•由于字符集中有6个字符,优先队列的大小初始为6,总共用5次合并得到最终的编码树T。
• 每次合并使Q的大小减1,最终得到的树就是最优前缀编码:哈夫曼编码树,每个字符的编码由树T的根到该字符的路径上各边的标号所组成。
1️⃣ 算法首先用字符集C中每一个字符c的频率f(c)初始化优先队列Q。以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。
2️⃣ 然后不断地从优先队列Q中取出具有最小频率的两棵树x和y,将它们合并为一棵新树z。z的频率是x和y的频率之和。
3️⃣ 新树z以x为其左儿子,y为其右儿子(也可以y为其左儿子,x为其右儿子。不同的次序将产生不同的编码方案,但平均码长是相同的)。经过n-1次的合并后,优先队列中只剩下一棵树,即所要求的树T。
4.Dijkstra算法—单源最短路径 #
给定带权有向图G=(V,E),其中每条边的权是非负实数。
给定V中的一个顶点,称为源。
现在要计算从源到其他所有各顶点的最短路径长度。这里的路径长度是指路径上各边权之和,这个问题通常称为单源最短路径问题。
考点:画一个迭代矩阵
算法基本思想 #
Dijkstra算法是求解单源最短路径问题的一个贪心算法。
基本思想:设置一个顶点集合S ,并不断地作贪心选择来扩充这个集合。一个顶点属于集合 S 当且仅当从源到该顶点的最短路径长度已知。
Dijkstra算法通过分步方法求出最短路径。
每一步产生一个到达新的目的顶点的最短路径。
下一步所能达到的目的顶点通过这样的贪心准则选取:在还未产生最短路径的顶点中,选择路径长度最短的目的顶点。
也就是说, Dijkstra算法按路径长度顺序产生最短路径。
Dijkstra算法的执行 #
1️⃣ 设置一个顶点集合S。一个顶点属于集合 S 当且仅当从源到该顶点的最短路径长度已知。
2️⃣ 初始时,S中仅含有源。
3️⃣ 设u是G的某一个顶点,把从源到u且中间只有经过S中顶点的路称为从源到u的特殊路径,并且用数组dist来记录当前每个顶点所对应的最短特殊路径长度。
4️⃣ Dijkstra算法每次从V-S中取出具有最短特殊路径长度的顶点u,将u添加到 S 中,同时对数组dist作必要的修改。
5️⃣ 一旦S包含了所有V中顶点,dist就记录了从源到所有其他顶点之间的最短路径长度。
过程说明 #
已知:带权有向图
V = { v1, v2, v3, v4, v5 }
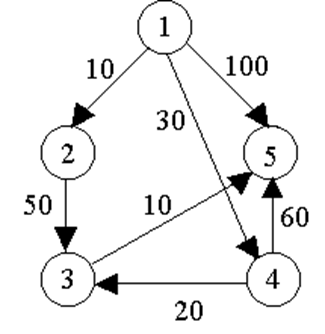
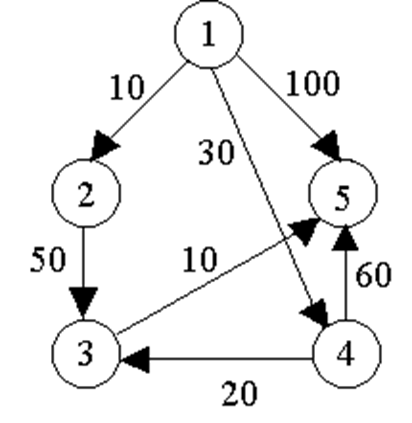
E = { < v1, v2 >, < v1, v4 >, < v1, v5 >, < v2, v3 >, < v3, v5 >, < v4, v3 >, < v4, v5 > }
设为v1源点,求其到其余顶点的最短路径。
其中,没有特殊路径的顶点用maxint表示其最短特殊路径长度
迭代矩阵(考点) #
可能会画这样的图,数据结构让画过。
| 迭代 | S | u | dist[2] | dist[3] | dist[4] | dist[5] |
|---|---|---|---|---|---|---|
| 初始 | {1} | - | 10 | maxint | 30 | 100 |
| 1 | {1,2} | 2 | 10 | 60 | 30 | 100 |
| 2 | {1,2,4} | 4 | 10 | 50 | 30 | 90 |
| 3 | {1,2,4,3} | 3 | 10 | 50 | 30 | 60 |
| 4 | {1,2,4,3,5} | 5 | 10 | 50 | 30 | 60 |
按长度顺序产生最短路径时,下一条最短路径总是由一条已产生的最短路径加上一条边形成。
没有优化的代码:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#define N 510
using namespace std;
int grid[N][N];
bool isInSet[N];
int minLen[N];
void dij(int n, int m){
memset(minLen, 0x3f, sizeof(minLen));
memset(isInSet, -1, sizeof(isInSet));
minLen[1] = 0;
for(int index = 0; index < n; ++index){
int t = -1;
//遍历找到距离最小的点
for(int i = 1; i <= n; ++i){
if(!isInSet[i] && (t == -1 || minLen[i] < minLen[t]))
t = i;
}
isInSet[t] = true;
//用t更新到所有其他点的距离
for(int i = 1; i <= n; ++i){
minLen[i] = min(minLen[i], minLen[t] + grid[t][i]);
}
}
int ans = (minLen[n] == 0x3f3f3f3f ? -1 : minLen[n]);
printf("%d\n", ans);
}
int main(void){
int n, m;
cin >> n >> m;
memset(grid, 0x3f, sizeof(grid));
for(int index = 0; index < m; ++index){
int x, y, z;
cin >> x >> y >> z;
grid[x][y] = min(grid[x][y], z);//去重复
}
dij(n, m);
}
使用堆来做优化:
const int N = 100010;
// 稀疏图用邻接表来存
int h[N], e[N], ne[N], idx;
int w[N]; // 用来存权重
int dist[N];
bool st[N]; // 如果为true说明这个点的最短路径已经确定
int n, m;
void add(int x, int y, int c)
{
// 有重边也不要紧,假设1->2有权重为2和3的边,再遍历到点1的时候2号点的距离会更新两次放入堆中
// 这样堆中会有很多冗余的点,但是在弹出的时候还是会弹出最小值2+x(x为之前确定的最短路径),
// 并标记st为true,所以下一次弹出3+x会continue不会向下执行。
w[idx] = c;
e[idx] = y;
ne[idx] = h[x];
h[x] = idx++;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap; // 定义一个小根堆
// 这里heap中为什么要存pair呢,首先小根堆是根据距离来排的,所以有一个变量要是距离,
// 其次在从堆中拿出来的时候要知道知道这个点是哪个点,不然怎么更新邻接点呢?所以第二个变量要存点。
heap.push({ 0, 1 }); // 这个顺序不能倒,pair排序时是先根据first,再根据second,
// 这里显然要根据距离排序
while(heap.size())
{
PII k = heap.top(); // 取不在集合S中距离最短的点
heap.pop();
int ver = k.second, distance = k.first;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i]; // i只是个下标,e中在存的是i这个下标对应的点。
if(dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({ dist[j], j });
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
5.最小生成树MST(算法大意要描述) #
1、问题描述 #
设G=(V,E)是无向带权连通图,即一个网络。
E中每条边(v,w)的权为𝑐[𝑣][𝑤]。如果G的子图G’是一棵包含G的所有顶点的树,则称G’为G的生成树。
生成树上各边权的总和称为该生成树的耗费。在G的所有生成树中,耗费最小的生成树称为G的最小生成树。
网络的最小生成树在实际中有广泛应用。
例如,在设计通信网络时,用图的顶点表示城市,用边(v,w)的权𝑐[𝑣][𝑤]表示建立城市v和城市w之间的通信线路所需的费用,则最小生成树就给出了建立通信网络的最经济的方案。
2、贪心法求解准则 #
根据最优量度标准,算法的每一步从图中选择一条符合准则的边,共选择n-1条边,构成无向连通图的一棵生成树。
贪心法求解的关键:该量度标准必须足够好。它应当保证依据此准则选出n-1条边构成原图的一棵生成树,必定是最小代价生成树。
3、prim算法 #
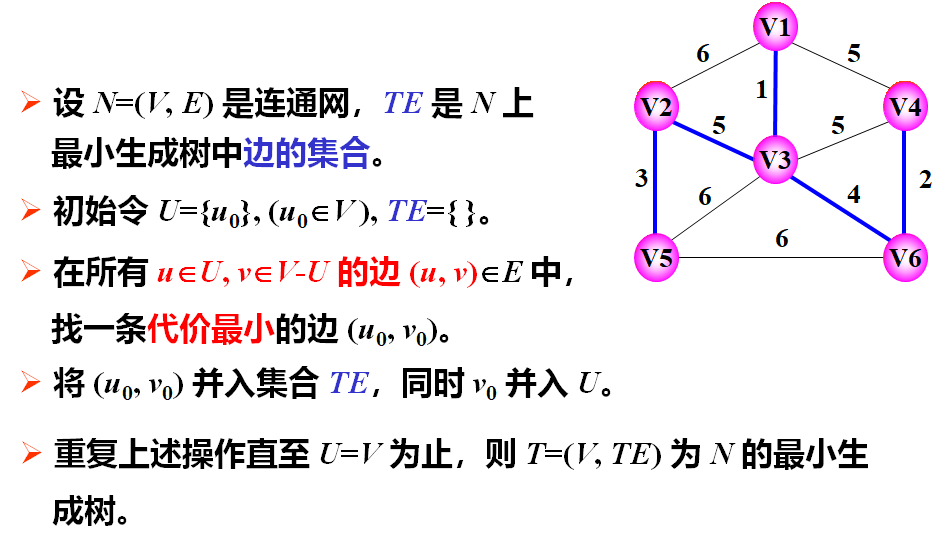
MST(Minimum Spanning Tree,最小生成树)问题有两种通用的解法,Prim算法就是其中之一,它是从点的方面考虑构建一颗MST,大致思想是:设图G顶点集合为U,首先任意选择图G中的一点作为起始点a,将该点加入集合V,再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小,此时将b点也加入集合V;以此类推,现在的集合V={a,b},再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小,此时将c点加入集合V,直至所有顶点全部被加入V,此时就构建出了一颗MST。因为有N个顶点,所以该MST就有N-1条边,每一次向集合V中加入一个点,就意味着找到一条MST的边。
详解请参考https://blog.csdn.net/yeruby/article/details/38615045
考点:算法思想与生成顺序方法说明
Kruskal算法的贪心准则:按边代价的非减次序考察E中的边,从中选择一条代价最小的边e=(u,v)。这种做法使得算法在构造生成树的过程中,当前子图不一定是连通的。
算法思想——从点出发
void Prim(int n,Type **c){//c[i][j]为边(i,j)的权值
TE=Ø;
U={1};
while(U!=V){
(u,v)=u属于U且v属于V-U的最小权边;
TE=TE∪{(u,v)};
U=U∪{v};
}
}
Prim算法的时间复杂度为𝑂(𝑛2)
4、Kruskal算法 #
从边的角度出发解决问题。
详情请看https://www.cnblogs.com/fzl194/p/8723325.html
算法思想——从边出发
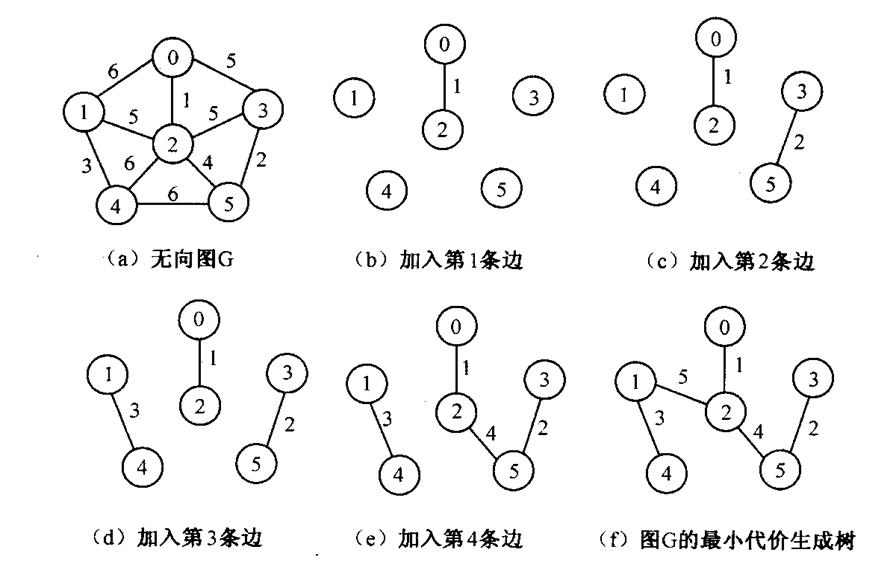
1️⃣设连通网 N = (V, E ),令最小生成树初始状态为只有 n 个顶点而无边的非连通图 T=(V, { }),每个顶点自成一个连通分量。
2️⃣在 E 中选取代价最小的边,若该边依附 的顶点落在 T 中相同的连通分量上(即: 不能形成环),则将此边加入到 T 中;否 则,舍去此边,选取下一条代价最小的边。
3️⃣ 依此类推,直至 T 中所有顶点都在同一 连通分量上为止。
Kruskal算法的时间复杂度为𝑂(𝑛𝑙𝑜𝑔𝑛)
6.*多机调度问题 #
近似算法,最长的最先开始处理即可。
1、问题描述 #
多机调度问题要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。约定,每个作业均可在任何一台机器上加工处理,但未完工前不允许中断处理。作业不能拆分成更小的子作业。
这个问题是NP完全问题,到目前为止还没有有效的解法。对于这一类问题,用贪心选择策略有时可以设计出较好的近似算法。
2、算法思想 #
采用最长处理时间作业优先的贪心选择策略可以设计出解多机调度问题的较好的近似算法。 按此策略,当𝑛≤𝑚时,只要将机器i的[0, ti]时间区间分配给作业i即可,算法只需要O(1)时间。 当𝑛>𝑚 时,首先将n个作业依其所需的处理时间从大到小排序。然后依此顺序将作业分配给空闲的处理机。算法所需的计算时间为O(nlogn)。
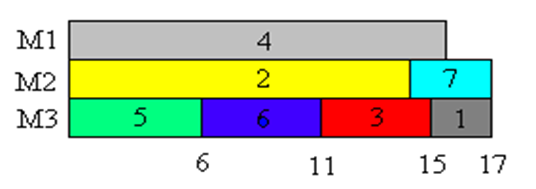
3、举例说明 #
设7个独立作业{1,2,3,4,5,6,7}由3台机器M1,M2和M3加工处理。各作业所需的处理时间分别为{2,14,4,16,6,5,3}。按算法greedy产生的作业调度如下图所示,所需的加工时间为17。
5.回溯算法 #
填空题会有代码填空,大题会手动回溯
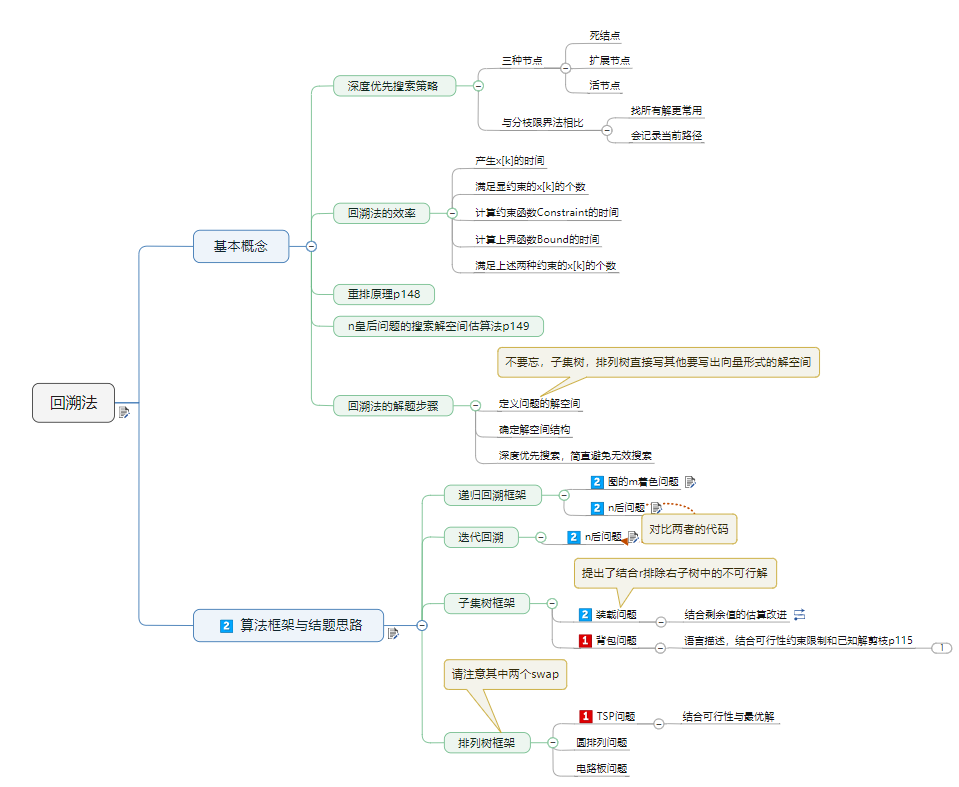
学习要点 #
理解回溯法的深度优先搜索策略。
掌握用回溯法解题的算法框架
(1)递归回溯
(2)迭代回溯
(3)子集树算法框架
(4)排列树算法框架
5.1 回溯法的算法框架 #
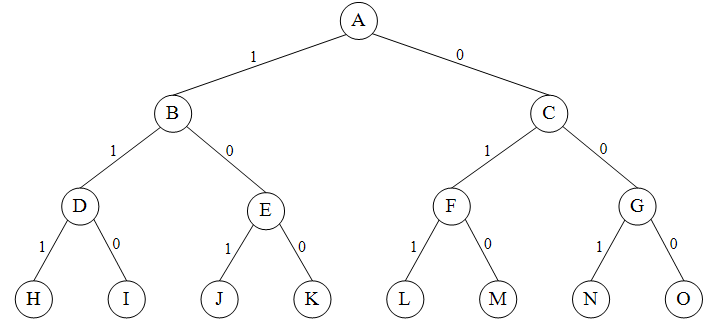
回溯法的基本做法是搜索,或是一种组织得井井有条的,能避免不必要搜索的穷举式搜索法。这种方法适用于解一些组合数相当大的问题。
回溯法在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时,先判断该结点是否包含问题的解。如果肯定不包含,则跳过对该结点为根的子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先策略搜索。
1、问题的解空间 #
用回溯法解问题时,应明确定义问题的解空间。
解空间往往用向量集表示。
问题的解向量:回溯法希望一个问题的解能够表示成一个n元式(x1,x2,…,xn)的形式。
显约束:对分量xi的取值限定。
隐约束:为满足问题的解而对不同分量之间施加的约束。
解空间:对于问题的一个实例,解向量满足显式约束条件的所有多元组,构成了该实例的一个解空间。
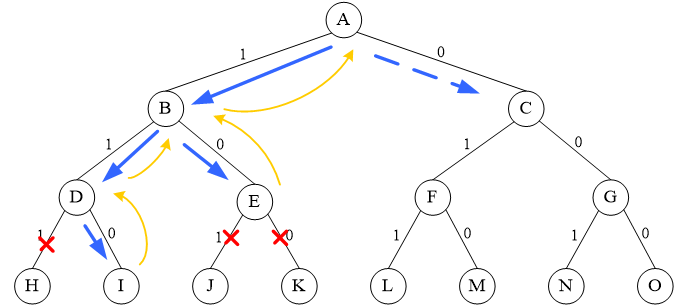
2、回溯的基本思想 #
扩展结点:一个正在产生儿子的结点称为扩展结点。
活结点:一个自身已生成但其儿子还没有全部生成的节点称做活结点。
死结点:一个所有儿子已经产生的结点称做死结点。
深度优先的问题状态生成法:如果对一个扩展结点R,一旦产生了它的一个儿子C,就把C当做新的扩展结点。在完成对子树C(以C为根的子树)的穷尽搜索之后,将R重新变成扩展结点,继续生成R的下一个儿子(如果存在)。
所以回溯法中一个节点是可以多次成为一个扩展节点但是分支限界法一个节点最多仅有一次机会。
宽度优先的问题状态生成法:在一个扩展结点变成死结点之前,它一直是扩展结点。
回溯法从开始结点(根结点)出发,以深度优先方式搜索整个解空间。
基本思想
1️⃣ 针对所给问题,定义问题的解空间;
2️⃣ 确定易于搜索的解空间结构;
3️⃣ 以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索
常用剪枝函数:(这里可能会考察定义)
用约束函数在扩展结点处剪去不满足约束的子树;
用限界函数剪去得不到最优解的子树。
3、递归回溯——背诵 #
void Backtrack (int t) //t为递归深度
{
if (t>n)
Output(x); //记录或输出可靠解x,x为数组
else
for (int i=f(n,t); i<=g(n,t); i++)
{
//f(n,t)表示在当前扩展结点处未搜索过的子树的起始编号
//g(n,t)为终止编号
x[t]=h(i); //h(i)表示当前扩展结点处x[t]的第i个可选值
if (Constraint(t)&&Bound(t)) //剪枝
Backtrack(t+1);
}
}
回溯法对解空间作深度优先搜索,因此,在一般情况下用递归方法实现回溯法。
4、迭代回溯——会填空即可 #
void IterativeBacktrack (){
int t=1;
while (t>0){
if (f(n,t)<=g(n,t))
for (int i=f(n,t); i<=g(n,t); i++){
x[t]=h(i);
if (Constraint(t)&&Bound(t)){
if (solution(t)) //判断是否已得到可行解
Output(x);
else
t++;
}
}
else
t--;
}
}
f(n,t)表示在当前扩展结点处未搜索过的子树的起始编号
g(n,t)为终止编号
h(i)表示当前扩展结点处x[t]的第i个可选值
5、子集树和排列树(重点) #
子集树:当所给的问题是从n个元素的集合S中找出满足某种性质的子集时,相应的解空间树称为子集树。时间复杂度𝛺(2𝑛)。算法描述如下:
LeetCode:https://leetcode.cn/problems/subsets/
class Solution {
List<Integer> path = new ArrayList();
List<List<Integer>> ans = new ArrayList();
public List<List<Integer>> subsets(int[] nums) {
dfs(0, nums);
return ans;
}
private void dfs(int index, int[] nums) {
if(index == nums.length){
ans.add(new ArrayList<Integer>(path));
return;
}
dfs(index + 1, nums);
path.add(nums[index]);
dfs(index + 1, nums);
path.remove(path.size() - 1);
}
}
类似于伪代码:
每个代码选和不选。
void Backtrack (int t)
{
if (t>n)
Output(x);
else
for (int i=0; i<=1; i++)
{
x[t]=i;
if (Constraint(t)&&Bound(t))
Backtrack(t+1);
}
}
排列树当所给的问题是确定n个元素满足某种性质的排列时,相应的解空间树称为排列树。时间复杂度𝛺(𝑛!)。算法描述如下:
时间复杂度就是排列的大小Ann = n!。
LeetCode:https://leetcode.cn/problems/permutations
class Solution {
List<List<Integer>> ans = new ArrayList();
public List<List<Integer>> permute(int[] nums) {
dfs(0, nums);
return ans;
}
private void swap(int i, int j, int[] nums){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
private void dfs(int index, int[] nums){
if(index == nums.length){
List<Integer> path = Arrays.stream(nums).boxed().collect(Collectors.toList());
ans.add(path);
return;
}
// 重点:在基准之后循环,交换,接着继续递归。
for(int i = index; i < nums.length; ++i){
swap(i, index, nums);
dfs(index + 1, nums);
swap(i, index, nums);
}
}
}
注意这里的两个swap函数。
void Backtrack (int t)
{
if (t>n)
Output(x);
else
for (int i=t; i<=n; i++)
{
Swap(x[t], x[i]);
if (Constraint(t)&&Bound(t))
Backtrack(t+1);
Swap(x[t], x[i]);
}
}
5.2 装载问题 #
1、问题描述 #
有一批共n个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i的重量为wi,且∑𝑖=1𝑛𝑤𝑖≤𝑐1+𝑐2,装载问题要求确定是否有一个合理的装载方案可将这些集装箱装上这2艘轮船。如果有,找出一种装载方案。
例如:
n=3, c1=c2=50,且w=[10,40,40]。
装载方案:
第一艘轮船装集装箱1和2;二艘轮船装集装箱3。
如果一个给定装载问题有解,则采用下面的策略可得到最优装载方案。(1)首先将第一艘轮船尽可能装满;(2)将剩余的集装箱装上第二艘轮船。将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集,使该子集中集装箱重量之和最接近c1。
2、算法分析 #
解空间:子集树
可行性约束函数(选择当前元素):∑𝑖=1𝑛𝑤𝑖𝑥𝑖≤𝑐1𝑥𝑖∈0,1
template<typename Type>
class Loading
{
template<typename T>
friend T MaxLoading(T [],T,int);
private:
void Backtrack(int i);
int n; //集装箱数
Type *w; //集装箱重量数组
Type c; //第1艘轮船的载重量
Type cw; //当前载重量
Type bestw; //当前最优载重量
};
template<typename Type>
void Loading<Type>::Backtrack(int i) //搜索第i层结点
{
if(i>n) //到达叶结点
{
if(cw>bestw)
bestw=cw;
return;
}
if(cw+w[i]<=c) //进入左子树,x[i]=1
{
cw+=w[i];
Backtrack(i+1); //继续搜索下一层
cw-=w[i]; //退出左子树
}
Backtrack(i+1); //进入右子树,x[i]=0
}
template<typename Type>
Type MaxLoading(Type w[],Type c,int n) //返回最优载重量
{
Loading<Type> X;
X.w=w; //初始化X
X.c=c;
X.n=n;
X.bestw=0;
X.cw=0;
X.Backtrack(1); //从第1层开始搜索
return X.bestw;
}
int main()
{
const int n=6;
int c=80;
int w[]={0,20,40,40,10,30,20}; //下标从1开始
int s=MaxLoading(w,c,n);
cout<<s<<endl;
return 0;
算法在每个结点处花费O(1)时间,子集树中结点个数为O(2n),故算法的计算时间为O(2n)。
3、上界函数 #
对于上一算法可引入一个上界函数,用于剪去不含最优解的子树。
上界函数(不选择当前元素):当前载重量cw+剩余集装箱的重量r≤当前最优载重量bestw。
就是剪枝函数。
template<typename Type>
class Loading
{
template<typename T>
friend T MaxLoading(T [],T,int);
private:
void Backtrack(int i);
int n; //集装箱数
Type *w; //集装箱重量数组
Type c; //第1艘轮船的载重量
Type cw; //当前载重量
Type bestw; //当前最优载重量
Type r; //剩余集装箱重量
};
template<typename Type>
void Loading<Type>::Backtrack(int i) //搜索第i层结点
{
if(i>n) //到达叶结点
{
if(cw>bestw)
bestw=cw;
return;
}
r-=w[i]; //剩余集装箱重量
if(cw+w[i]<=c) //进入左子树,x[i]=1
{
cw+=w[i];
Backtrack(i+1); //继续搜索下一层
cw-=w[i]; //退出左子树
}
if(cw+r>bestw) //上界函数
//进入右子树,x[i]=0
Backtrack(i+1);
r+=w[i];
}
4、构造最优解 #
为构造最优解,需在算法中记录与当前最优值相应的当前最优解。
在类Loading中增加两个私有数据成员:
int* x:用于记录从根至当前结点的路径;
int* bestx:记录当前最优解。
算法搜索到叶结点处,就修正bestx的值。
public class Loading {
// 船最大装载问题
private int n;// 集装箱数
private int[] x;// 当前解
private int[] bestx;// 当前最优解
private int[] w;// 集装箱重量数组
private int c;// 第一艘船的载重量
private int cw;// 当前载重量
private int bestw;// 当前最优载重量
private int r;// 剩余集装箱重量
void backTrack(int i)// 搜索第i层结点
{
if (i > n) {
// 到达叶结点
if (cw > bestw) {
for (int j = 1; j <= n; j++) {
bestx[j] = x[j];
}
bestw = cw;
}
return;
}
r -= w[i];
// 剩余集装箱重量
if (cw + w[i] <= c) {
// 进入左子树
x[i] = 1;
// 装第i个集装箱
cw += w[i];
backTrack(i + 1);
// 进入下一层
cw -= w[i];
// 退出左子树
}
if (cw + r > bestw) {
// 进入右子树
x[i] = 0;
// 不装第i个集装箱
backTrack(i + 1);
}
r += w[i];
}
public Loading(int[] w, int c, int n, int[] bestx) {
this.w = w;
this.c = c;
this.n = n;
this.bestx = bestx;
this.bestw = 0;
this.cw = 0;
for (int i = 1; i <= n; i++) {
this.r += w[i];
}
this.x = new int[n + 1];
}// 构造器
public static void main(String[] args) {
int n = 5;
int c = 10;
int w[] = {0, 7, 2, 6, 5, 4};// 下标从1开始
int bestx[] = new int[n + 1];
Loading test = new Loading(w, c, n, bestx);
test.backTrack(1);
for (int i = 1; i <= n; i++) {
System.out.print(bestx[i] + " ");
}
System.out.println();
System.out.println(test.bestw);
return;
}
}
由于bestx可能被更新O(2n)次,故算法的时间复杂性为O(n2^n)。
5、迭代回溯(填空即可) #
理解循环遍历的原理。
由于数组x记录了解空间树中从根到当前扩展结点的路径,利用这些信息,可将上述回溯法表示成非递归的形式。
n=3, c1=c2=50,且w=[10,40,40]
//迭代回溯法,返回最优载重量
template<typename Type>
Type MaxLoading(Type w[],Type c,int n,int bestx[])
{
//初始化根结点
int i=1;
int *x=new int[n+1];
Type bestw=0;
Type cw=0;
Type r=0;
for(int j=1;j<=n;j++)
r+=w[j];
while(true) //搜索子树
{
while(i<=n&&cw+w[i]<=c) //进入左子树,条件为真,则一直往左搜索
{
r-=w[i];
cw+=w[i];
x[i]=1;
i++;
}
if(i>n) //到达叶结点
{
for(int j=1;j<=n;j++)
bestx[j]=x[j];
bestw=cw;
}
else //进入右子树
{
r-=w[i];
x[i]=0;
i++;
}
while(cw+r<=bestw) //剪枝回溯
{
i--;
while(i>0&&!x[i]) //从右子树返回
{
r+=w[i];
i--;
}
if(i==0) //如返回到根,则结束
{
delete[] x;
return bestw;
}
//进入右子树
x[i]=0;
cw-=w[i];
i++;
}
}
}
算法的计算时间为O(2^n)。
5.3 n皇后问题(重点,三个函数都要掌握) #
LeetCode:https://leetcode.cn/problems/n-queens/description/
N皇后本质还是排列的问题。
详细的解答:https://leetcode.cn/problems/n-queens/solutions/2079586/hui-su-tao-lu-miao-sha-nhuang-hou-shi-pi-mljv/
1、问题描述 #
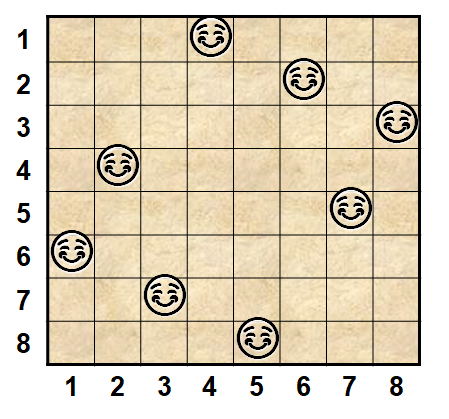
在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。
2、算法设计 #
解向量:(x1,x2,…,xn)
用n元组x[1:n]表示n后问题的解,其中x[i]表示皇后i放在棋盘的第i行的第x[i]列。
显约束:xi=1,2,…,n(能取值的范围)
隐约束:(两个皇后之间不能相互攻击)
不同列:xi≠xj
不处于同一正反对角线:|i-j|≠|xi-xj|
回溯法解n后问题时,用完全n叉树表示解空间,用可行性约束Place()剪去不满足行、列和斜线约束的子树。
Backtrack(i)搜索解空间中第i层子树。
sum记录当前已找到的可行方案数。
3、四皇后问题 #
问题描述
在4 x 4棋盘上放上4个皇后,使皇后彼此不受攻击。不受攻击的条件是彼此不在同行(列)、斜线上。求出全部的放法。
解表示
解向量: 4元向量X=(x1,x2,x3,x4), xi 表示皇后i放在i行上的列号,如(3,1,2,4)
解空间:{(x1,x2,x3,x4)|xi∈S,i=1~4}S={1,2,3,4}
可行性约束函数
显约束: xi∈S,i=1~4
隐约束(i ≠ j):xi ≠ xj (不在同一列)
|i-xi|≠|j-xj| (不在同一斜线)
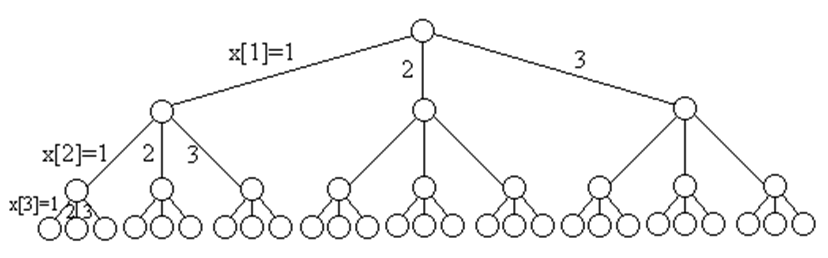
四皇后问题的解空间树是一棵完全4叉树,树的根结点表示搜索的初始状态,从根结点到第2层结点对应皇后1在棋盘中第1行的可能摆放位置,从第2层结点到第3层结点对应皇后2在棋盘中第2行的可能摆放位置,依此类推。
4、算法实现 #
public class nQueen {
//n皇后问题
private int n;//皇后个数
private int[] x;//当前解
private long sum;//当前已找到可行方案数
public nQueen(int n){
this.n = n;
this.sum = 0;
this.x = new int[n+1];
for (int i = 0; i <=n ; i++) {
x[i]=0;
}
this.backTrack(1);
}
/**
* 放置在第k行
*
* @param k
* @return 是否可行
*/
private boolean place(int k) {
for (int i = 1; i < k; i++) {
//前面有没有可能存在某一行在斜对角上产生冲突的状况
if (Math.abs(k - i) == Math.abs(x[k] - x[i]) || x[i] == x[k]) {
//
return false;
}
}
return true;
}
/**
* 递归回溯
* @param t
*/
public void backTrack(int t) {
if (t > n)
sum++;
else
for (int i = 1; i <= n; i++) {//[1:n]列
x[t] = i;//放在第i列
if (place(t))
backTrack(t + 1);
}
}
}
优化:
class Solution {
public List<List<String>> solveNQueens(int n) {
List<List<String>> ans = new ArrayList<>();
int[] queens = new int[n]; // 皇后放在 (r,queens[r])
boolean[] col = new boolean[n];
boolean[] diag1 = new boolean[n * 2 - 1];
boolean[] diag2 = new boolean[n * 2 - 1];
dfs(0, queens, col, diag1, diag2, ans);
return ans;
}
private void dfs(int r, int[] queens, boolean[] col, boolean[] diag1, boolean[] diag2, List<List<String>> ans) {
int n = col.length;
if (r == n) {
List<String> board = new ArrayList<>(n); // 预分配空间
for (int c : queens) {
char[] row = new char[n];
Arrays.fill(row, '.');
row[c] = 'Q';
board.add(new String(row));
}
ans.add(board);
return;
}
// 在 (r,c) 放皇后
for (int c = 0; c < n; c++) {
int rc = r - c + n - 1;
if (!col[c] && !diag1[r + c] && !diag2[rc]) { // 判断能否放皇后
queens[r] = c; // 直接覆盖,无需恢复现场
col[c] = diag1[r + c] = diag2[rc] = true; // 皇后占用了 c 列和两条斜线
dfs(r + 1, queens, col, diag1, diag2, ans);
col[c] = diag1[r + c] = diag2[rc] = false; // 恢复现场
}
}
}
}
非递归的回溯方法:
先暂时能看懂就行。
/**
* 非递归回溯
*
* @param t
*/
public void backTrack_o(int t) {
x[1] = 0;
int k = 1;
while (k > 0) {
x[k] += 1; //第k行的放到下一列
//x[k]不能放置,则放到下一列,直到可放置
while ((x[k] <= n) && !place(k))
x[k] += 1;
if (x[k] <= n) //放在n列范围内
if (k == n) //已放n行
sum++;
else //不足n行
{
k++; //放下一行
x[k] = 0; //下一行又从第0列的下列开始试放
}
else //第k行无法放置,则重新放置上一行(放到下一列)
k--;
}
}
5.4 0-1背包问题(重点) #
1、算法描述 #
解空间:子集树
0-1背包问题是子集选取问题,其解空间可用子集树表示。
可行性约束函数:∑𝑖=1𝑛𝑤𝑖𝑥𝑖≤𝑐1
上界约束:当右子树中有可能包含最优解时才进入右子树搜索,否则剪去右子树。
设r是当前剩余物品价值总和,cp是当前价值,bestp是当前最优价值,当cp+r≤bestp时,剪去右子树。
计算右子树中解的上界更好的方法是将剩余的物品依其单位重量价值排序,然后依次装入物品,直到装不下时,再装入该物品一部分而装满背包,由此得到的价值是右子树中解的上界。——将背包问题作为0-1背包问题的上界。
2、算法实现 #
template<typename Typew,typename Typep>
class Knap
{
friend Typep Knapsack<>(Typep *,Typew *,Typew,int);
//<>指明友员函数为模板函数
private:
Typep Bound(int i); //计算上界
void Backtrack(int i);
Typew c; //背包容量
int n; //物品数
Typew *w; //物品重量数组
Typep *p; //物品价值数组
Typew cw; //当前重量
Typep cp; //当前价值
Typep bestp; //当前最优价值
};
template<typename Typew,typename Typep>
void Knap<Typew,Typep>::Backtrack(int i) //回溯
{
if(i>n)
{
bestp=cp;
return;
}
if(cw+w[i]<=c) //进入左子树
{
cw+=w[i];
cp+=p[i];
Backtrack(i+1);
cw-=w[i];
cp-=p[i];
}
if(Bound(i+1)>bestp) //进入右子树
Backtrack(i+1);
}
template<typename Typew,typename Typep>
Typep Knap<Typew,Typep>::Bound(int i) //计算上界
{
Typew cleft=c-cw; //剩余的背包容量
Typep b=cp; //b为当前价值
while(i<=n&&w[i]<=cleft) //依次装入单位重量价值高的整个物品
{
cleft-=w[i];
b+=p[i];
i++;
}
if(i<=n) //装入物品的一部分
b+=p[i]*cleft/w[i];
return b; //返回上界
}
class Object //物品类
{
friend int Knapsack(int *,int *,int,int);
public:
int operator <(Object a) const
{
return (d>a.d);
}
int ID; //物品编号
float d; //单位重量价值
};
template<typename Typew,typename Typep>
Typep Knapsack(Typep p[],Typew w[],Typew c,int n)
{
Typew W=0; //总重量
Typep P=0; //总价值
Object* Q=new Object[n]; //创建物品数组,下标从0开始
for(int i=1;i<=n;i++) //初始物品数组数据
{
Q[i-1].ID=i;
Q[i-1].d=1.0*p[i]/w[i];
P+=p[i];
W+=w[i];
}
if(W<=c) //能装入所有物品
return P;
QuickSort(Q,0,n-1); //依物品单位重量价值非增排序
Knap<Typew,Typep> K;
K.p=new Typep[n+1];
K.w=new Typew[n+1];
for(int i=1;i<=n;i++)
{
K.p[i]=p[Q[i-1].ID];
K.w[i]=w[Q[i-1].ID];
}
K.cp=0;
K.cw=0;
K.c=c;
K.n=n;
K.bestp=0;
K.Backtrack(1);
delete[] Q;
delete[] K.w;
delete[] K.p;
return K.bestp;
}
计算上界需要O(n)时间,最坏情况下有𝑂(2𝑛)个右儿子结点需要计算上界,故算法所需要的时间为𝑂(𝑛2𝑛)
5.5 图的m着色问题 #
比较简单,主要就写一个判定函数检查颜色是否可用。
1、问题描述 #
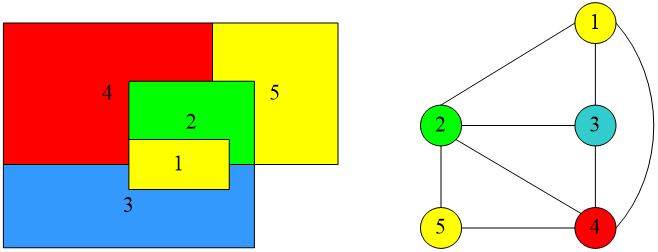
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色,每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。
这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色,则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。
2、算法设计 #
用图的邻接矩阵a表示无向连通图G。
解向量:(x1, x2, … , xn)表示顶点i所着颜色x[i]
可行性约束函数:顶点i与已着色的相邻顶点颜色不重复。
注意解空间树的画法。
class Color
{
friend int mColoring(int,int,int **);
private:
bool OK(int k); //检查颜色是否可用
void Backtrack(int t);
int n; //图的顶点数
int m; //可用颜色数
int **a; //图的邻接矩阵
int *x; //当前解
long sum; //当前已找到的可m着色方案数
};
bool Color::OK(int k) //检查顶点k颜色是否可用
{
for(int j=1;j<=n;j++){
if((a[k][j]==1)&&(x[j]==x[k])) //有边相连且两顶点颜色相同
return false;
}
return true;
}
void Color::Backtrack(int t)
{
if(t>n)
{
sum++;
for(int i=1;i<=n;i++)
cout<<x[i]<<' ';
cout<<endl;
}
else
for(int i=1;i<=m;i++) //m种颜色
{
x[t]=i; //顶点t使用颜色i
if(OK(t))
Backtrack(t+1);
x[t]=0; //恢复x[t]的初值
}
}
int mColoring(int n,int m,int **a)
{
Color X;
//初始化X
X.n=n;
X.m=m;
X.a=a;
X.sum=0;
int *p=new int[n+1];
for(int i=0;i<=n;i++)
p[i]=0;
X.x=p;
X.Backtrack(1);
delete[] p;
return
}
3、算法效率 #
时间耗费𝑂(𝑛𝑚𝑛)
判断下图是否是3可着色
尝试着画一下。
5.6 TSP问题(旅行售货员问题)【一级重点】 #
本问题相当重要,务必吃透。
1、算法描述 #
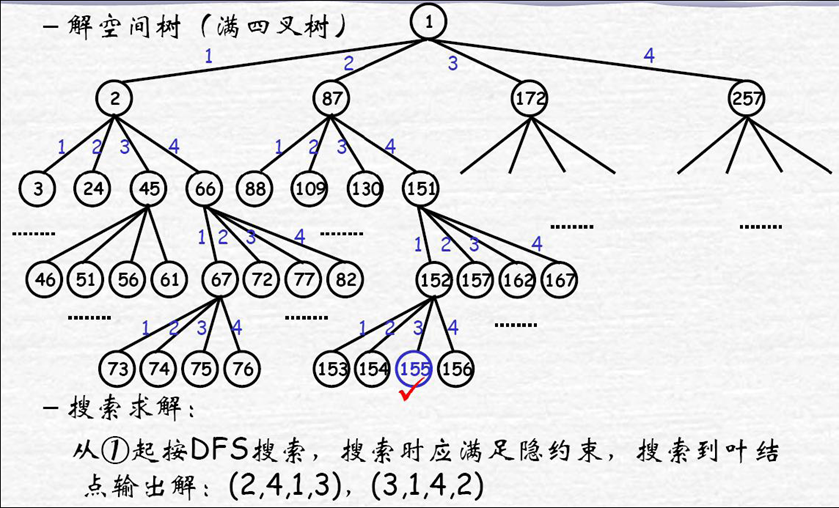
已给一个n个点的完全图,每条边都有一个长度,求总长度最短的经过每个顶点正好一次的封闭回路
因为每两个节点之间都是可达的,那么就是一个排列树。
解空间:排列树
开始时x=[1,2,…,n],则相应的排列树由x[1:n]的所有排列构成。
2、递归算法 #
当i=n时,当前扩展结点是排列树的叶结点的父结点,此时检查图G是否存在一条从顶点x[n-1]到顶点x[n]的边和一条从顶点x[n]到顶点1的边,如果两条边都存在,则找到一条回路。再判断此回路的费用是否优于当前最优回路的费用,是则更新当前最优值和最优解。
当i<n时,当前扩展结点位于排列树的第i-1层。图G中存在从顶点x[i-1]到x[i]的边时,检查x[1:i]的费用是否小于当前最优值,是则进入排列树的第i层,否则剪去相应子树。
3、算法实现 #
public class TSP {
/**
* 已给一个n个点的[完全图]),每条边都有一个长度,
* 求总长度最短的经过每个顶点正好一次的封闭回路
*/
private int n;//图的顶点数
private int[] x;//当前解
private int[] bestx;//当前最优解
private int[][] a;//邻接矩阵
private int cc;//当前费用
private int bestc;//当前最优值
private static final int NO_EDGE = Integer.MAX_VALUE;//无边标记
public TSP(int[][] a, int[] v, int n) {
this.a = a;
this.n = n;
this.bestx = v;
this.x = new int[n + 1];
this.bestc=NO_EDGE;
this.cc = 0;
this.backTrack(2);
}
public void backTrack(int i) {
// 什么时候收获结果?
if (i == n) {
//当i=n时,当前扩展结点是排列树的叶结点的父结点,此时检查图G是否存在一条从
// 顶点x[n-1]到顶点x[n]的边和一条从顶点x[n]到顶点1的边,如果两条边都存在,
// 则找到一条回路。再判断此回路的费用是否优于当前最优回路的费用,是则更新当前最优值和最优解。
if (a[x[n - 1]][x[n]] != NO_EDGE && a[x[n]][1] != NO_EDGE &&
(cc + a[x[n - 1]][x[n]] + a[x[n]][1] < bestc || bestc == NO_EDGE)) {
for (int j = 1; j <= n; j++) {
bestx[j] = x[j];
}
bestc = cc + a[x[n - 1]][x[n]] + a[x[n]][1];
}
} else {
//当i<n时,当前扩展结点位于排列树的第i-1层。图G中存在从顶点x[i-1]到x[i]的边时,
// 检查x[1:i]的费用是否小于当前最优值,是则进入排列树的第i层,否则剪去相应子树。
// 1.自己到自己节点在邻接矩阵中设置为无穷,肯定不会直接回去
// 2.也相当于是一种限制条件
for (int j = i; j <= n; j++) {
if (a[x[i - 1]][x[j]] != NO_EDGE && (cc + a[x[i - 1]][x[j]] < bestc || bestc == NO_EDGE)) {
// 注意这里要先交换,i之前的就是我们选择走的路径,i之后的是我们没走过的路径。
swap(x,i,j);
cc += a[x[i - 1]][x[i]];
backTrack(i + 1);
cc -= a[x[i - 1]][x[i]];
swap(x,i,j);
}
}
}
}
private void swap(int[]a, int x, int y) {
int temp = a[x];
a[x] = a[y];
a[y] = a[temp];
}
}
4、算法效率 #
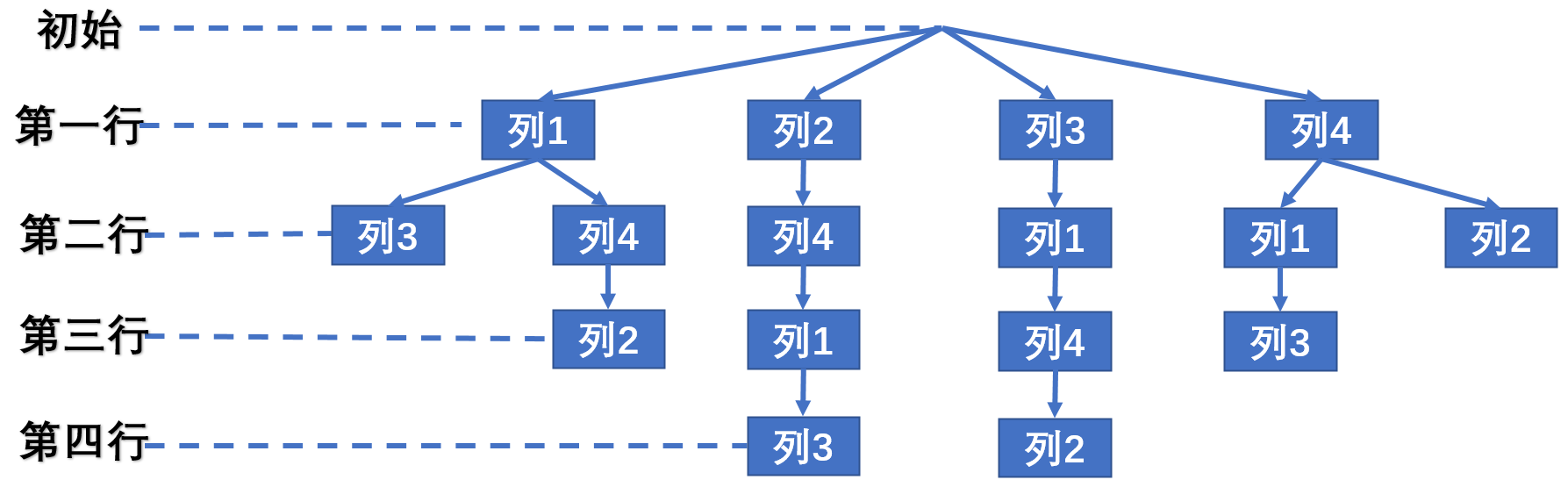
这是排列树,就是O(n!)
算法backtrack在最坏情况下可能需要更新当前最优解O((n-1)!)次,每次更新bestx需计算时间O(n),从而整个算法的计算时间复杂性为O(n!)。
5.7 最大团问题 #
最大团问题 给定无向图G=(V,E)。如果UV,且对任意u,vU有 (u,v)E,则称U是G的完全子图。例如{1,2}。 G的完全子图U是G的团当且仅当U不包含在G的更大的完全 子图中,例如{1,2,5}。 G的最大团是指G中所含顶点数最多的团。
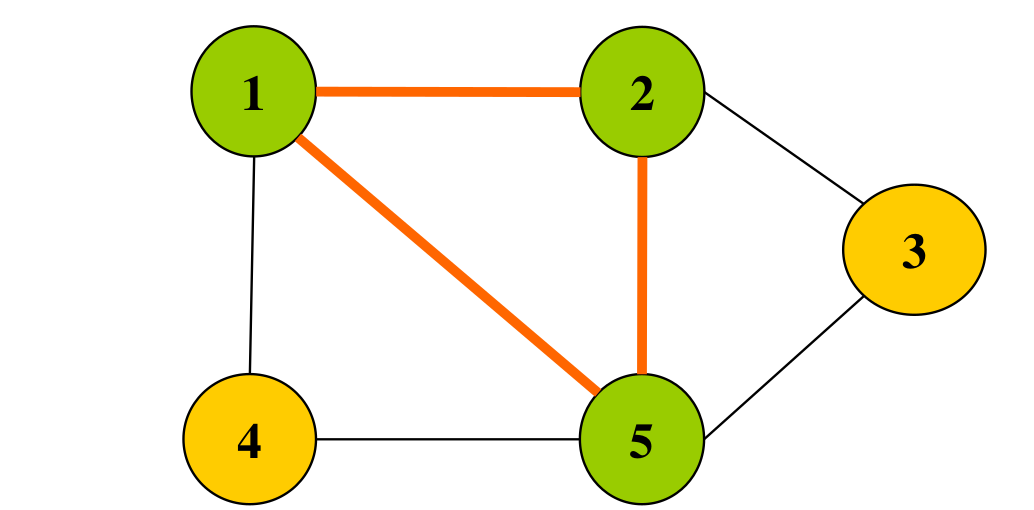
找出一个图的最大团: 可看做图G的顶点集V的子集选取问题。 • 解空间:子集树 • 可行性约束函数:顶点i到已选入顶点集中的每一个顶点都有边相连。 •上界函数:有足够多的可选择顶点使得算法有可能在右子树中找到更大的团。
代码:
x[]保存了团内的节点。
a [ i ] [ j ] 是boolean数组,表示其中的两个点有没有相连接。
每到一个新的节点,遍历检查这个节点有没有和现存的团中的每一个节点相连接,连接了我们就要了这个节点,否则不要。

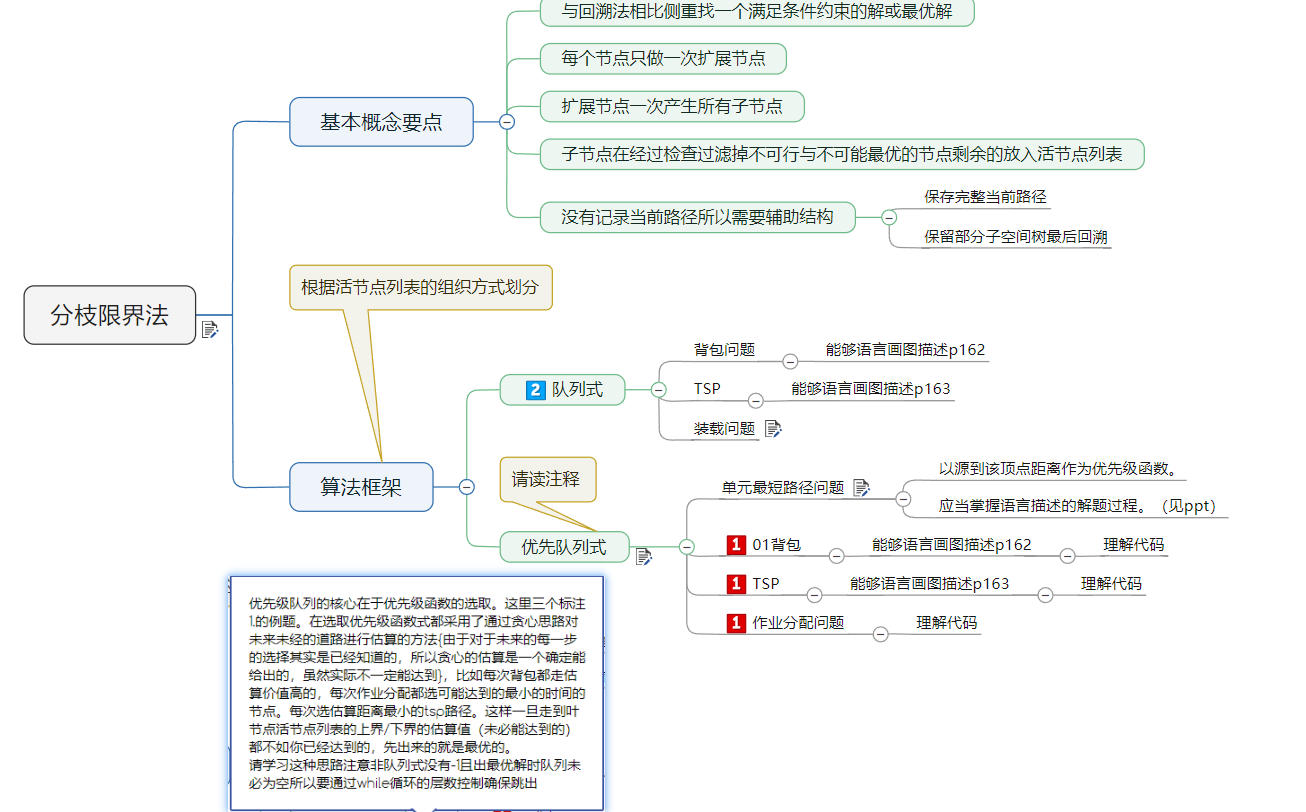
6.分支限界法 #
注意这里的基本概念要点。
6.1 分支限界法的基本思想 #
分支限界法和回溯法 #
区别是考试的重点。
求解目标:回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解。
搜索方式的不同:回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。
仅从方式来看,这类似于层序遍历的过程。
在分支限界法中,每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。
选择下一个E结点的方法如下:
1)先进先出(FIFO):从活结点表中取出结点的顺序与加入结点的顺序相同。
后进先出(LIFO):从活结点表中取出结点的顺序与加入结点的顺序相反。
2)优先队列式分支限界法
按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。
(就是Dijkstra的堆优化算法)
基本思想 #
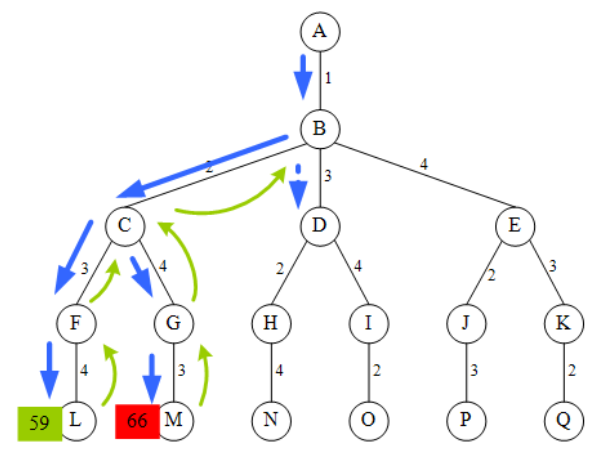
1️⃣ 在 e_结点估算沿着它的各儿子结点搜索时,目标函数可能取得的“界”,
2️⃣ 把儿子结点和目标函数可能取得的“界”,保存在优先队列或堆中,
3️⃣ 从队列或堆中选取“界”最大或最小的结点向下搜索,直到叶子结点,
4️⃣ 若叶子结点的目标函数的值,是结点表中的最大值或最小值,则沿叶子结点到根结点的路径所确定的解,就是问题的最优解,否则转 3 继续搜索
示例 #
0-1背包问题
考虑实例n=4,w=[3,5,2,1],v=[9,10,7,4],C=7。
定义问题的解空间
该实例的解空间为(x1,x2,x3,x4),xi=0或1(i=1,2,3,4)。
确定问题的解空间组织结构
该实例的解空间是一棵子集树,深度为4。
搜索解空间
约束条件
限界条件 cp+rp>bestp
队列式分支限界法 #
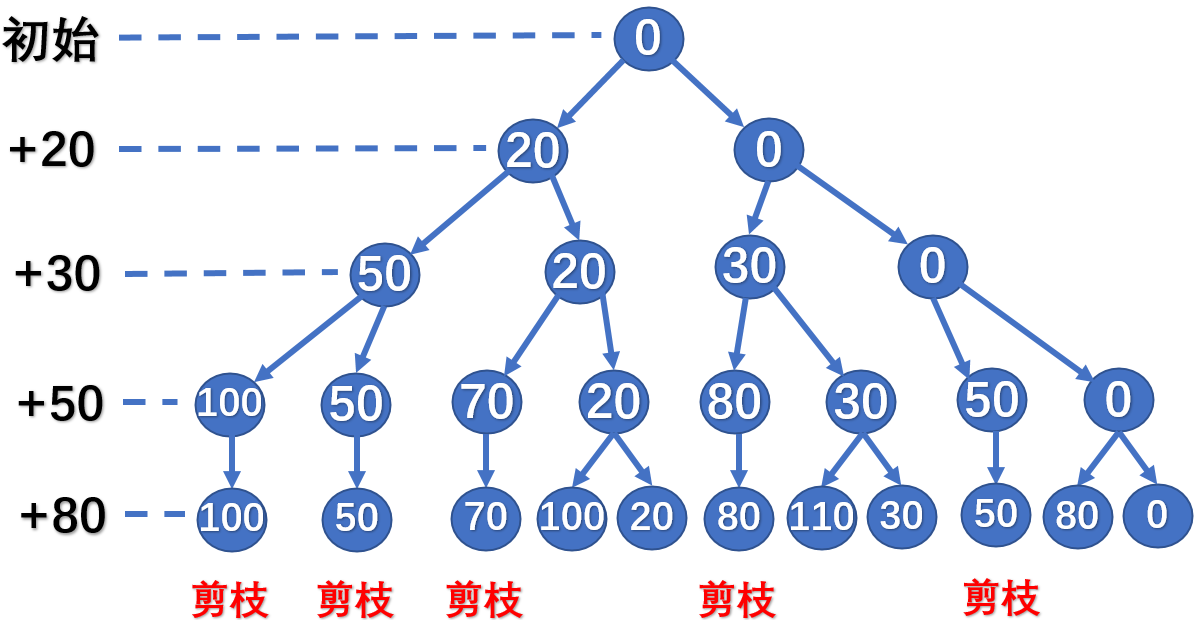
cp初始值为0;rp初始值为所有物品的价值之和;bestp表示当前最优解,初始值为0。
当cp>bestp时,更新bestp为cp。
理解下面的图:这样的过程就是类似于层序遍历生成一颗树。
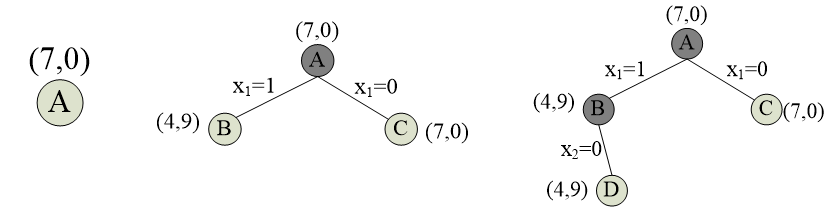
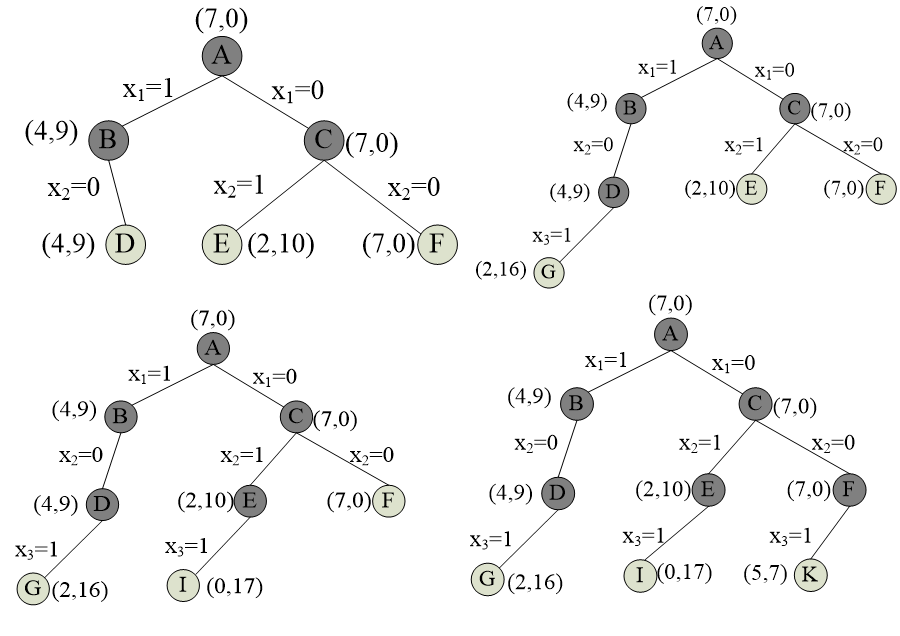
优先队列式 #
优先级:活结点代表的部分解所描述的装入背包的物品价值上界,该价值上界越大,优先级越高。活结点的价值上界up=cp+rp。
约束条件:同队列式
限界条件:up=cp+r‘p>bestp。
rp 剩余物品装满背包的价值
优先去装原来价值就更大的背包。
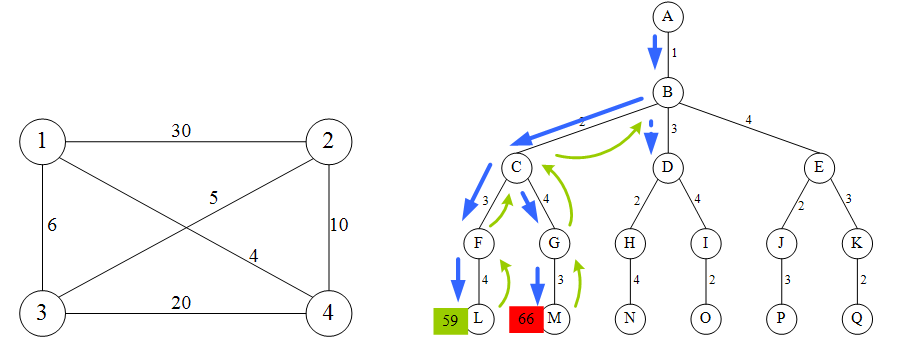
6.2 单源最短路径问题 #
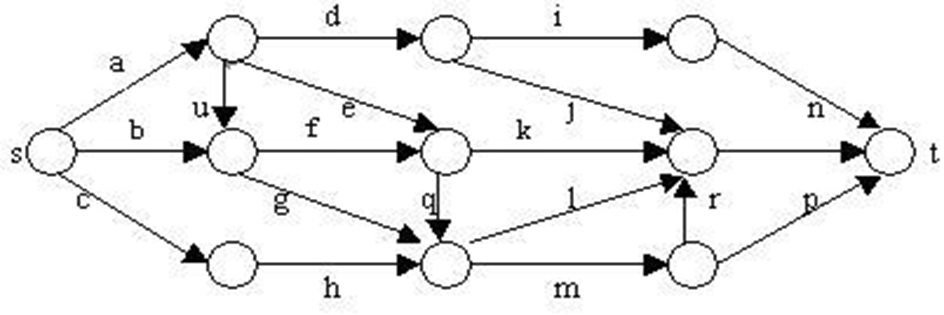
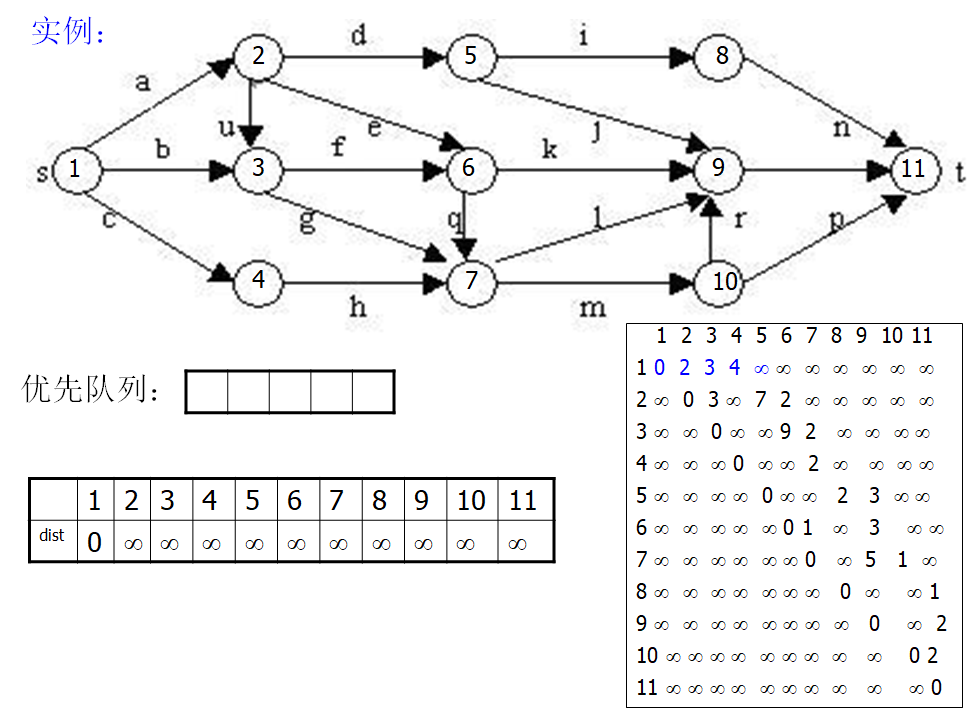
问题描述 #
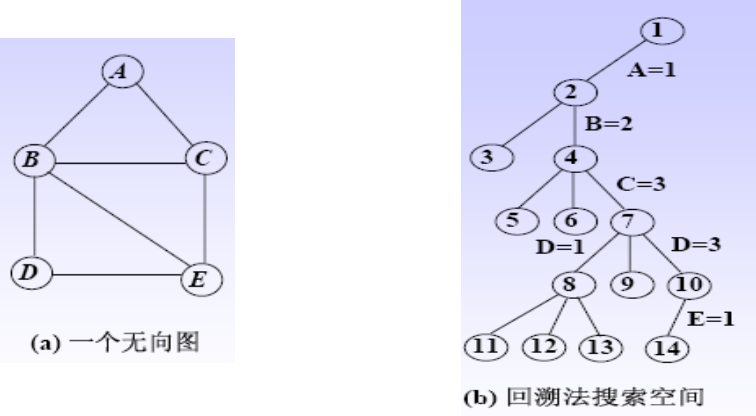
在下图所给的有向图G中,每一边都有一个非负边权。要求图G的从源顶点s到目标顶点t之间的最短路径。
下图是用优先队列式分支限界法解有向图G的单源最短路径问题产生的解空间树。其中,每一个结点旁边的数字表示该结点所对应的当前路长。
算法思想 #
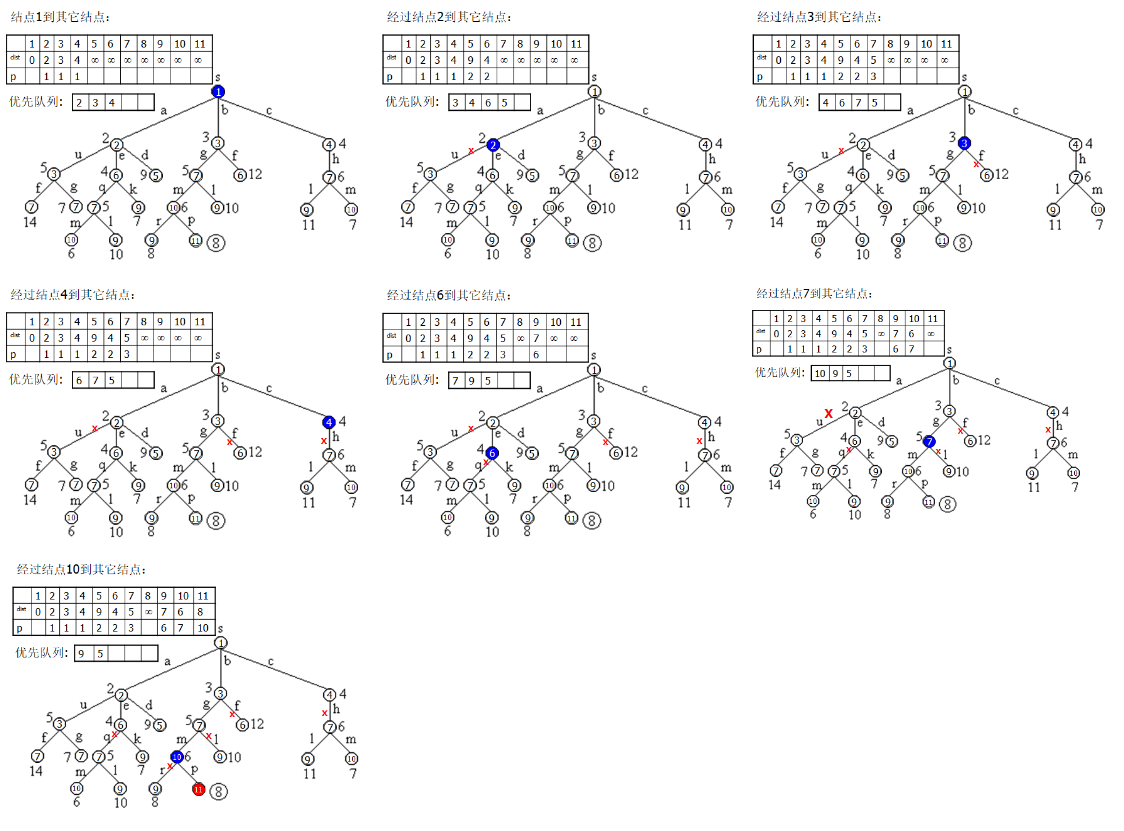
解单源最短路径问题的优先队列式分支限界法用一极小堆来存储活结点表。其优先级是结点所对应的当前路长。
算法从图G的源顶点s和空优先队列开始。结点s被扩展后,它的儿子结点被依次插入堆中。此后,算法从堆中取出具有最小当前路长的结点作为当前扩展结点,并依次检查与当前扩展结点相邻的所有顶点。
如果从当前扩展结点i到顶点j有边可达,且从源出发,途经顶点i再到顶点j的所相应的路径的长度小于当前最优路径长度,则将该顶点作为活结点插入到活结点优先队列中。这个结点的扩展过程一直继续到活结点优先队列为空时为止。
实例说明 #
算法设计 #
static float[][]a //图G的邻接矩阵
static float []dist //源到各顶点的距离
static int []p //源到各顶点的路径上的前驱顶点
HeapNode //最小堆元素
{ int i; //顶点编号
float length;//当前路长
……
}
//1.先进行一个while(true)的循环。
while (true) {//搜索问题的解空间
//2.取堆的最上面的节点出来并且对于每个点都进行一次遍历和更新。
for (int j = 1; j <= n; j++)
//3.如果满足条件的话就更改值并且加入优先队列。
if ((a[enode.i][j]<Float.MAX_VALUE)&&
(enode.length+a[enode.i][j]<dist[j])) {//顶点i和j间有边,且此路径长小于原先从原点到j的路径长
// 顶点i到顶点j可达,且满足控制约束
dist[j]= enode.length+c[enode.i][j];
p [j]= enode.i;
// 加入活结点优先队列
HeapNode node=new HeapNode(j,dist[j]);
heap.put(node);
}
// 取下一扩展结点
if ( heap.isEmpty( ) ) break;
else enode=(HeapNode)heap.removeMin();
}
}
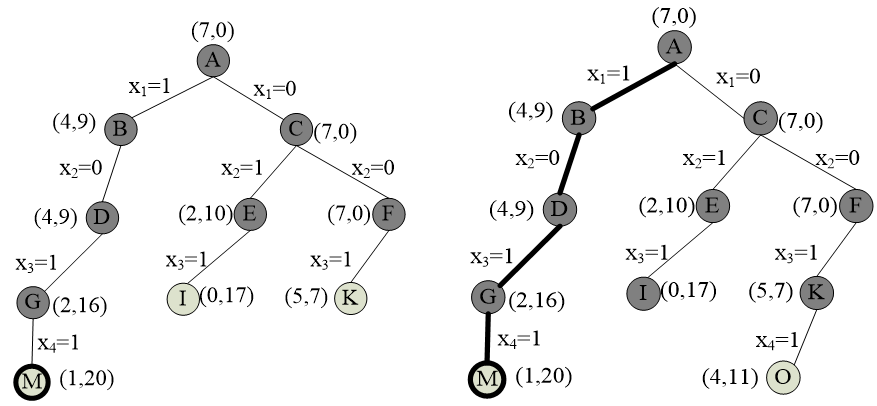
6.3 0-1背包问题[重点] #
解答参考https://www.it610.com/article/1296236014334976000.htm
问题描述 #
- 给定n种物品和一个背包。物品i的重量是wi,其价值为vi,背包的容量为c。
- 应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
- 在选择装入背包的物品时,对每种物品i只有2种选择,即装入背包或不装入背包。不能将物品i装入背包多次,也不能只装入部分的物品i。
算法的思想 #
- 首先,要对输入数据进行预处理,将各物品依其单位重量价值从大到小进行排列。
- 在实现时,由Bound计算当前结点处的上界。在解空间树的当前扩展结点处,仅当要进入右子树时才计算右子树的上界Bound,以判断是否将右子树剪。进入左子树时不需要计算上界,因为其上界与其父节点上界相同。
- 在优先队列分支限界法中,结点的优先级定义为:以结点的价值上界作为优先级(由bound函数计算出)
步骤 #
就是使用队列的同时还加上了附加条件。
- 算法首先根据基于可行结点相应的子树最大价值上界优先级,从堆中选择一个节点(根节点)作为当前可扩展结点。
- 检查当前扩展结点的左儿子结点的可行性。
- 如果左儿子结点是可行结点,则将它加入到子集树和活结点优先队列中。
- 当前扩展结点的右儿子结点一定是可行结点,
仅当右儿子结点满足上界函数约束时,才将它加入子集树和活结点优先队列。 - 当扩展到叶节点时,算法结束,叶子节点对应的解即为问题的最优值。
样例 #
假设有4个物品,其重量分别为(4, 7, 5, 3),价值分别为(40, 42, 25, 12),背包容量W=10。将给定物品按单位重量价值从大到小排序,结果如下:
| 物品 | 重量(w) | 价值(v) | 价值/重量(v/w) |
|---|---|---|---|
| 1 | 4 | 40 | 10 |
| 2 | 7 | 42 | 6 |
| 3 | 5 | 25 | 5 |
| 4 | 3 | 12 | 4 |
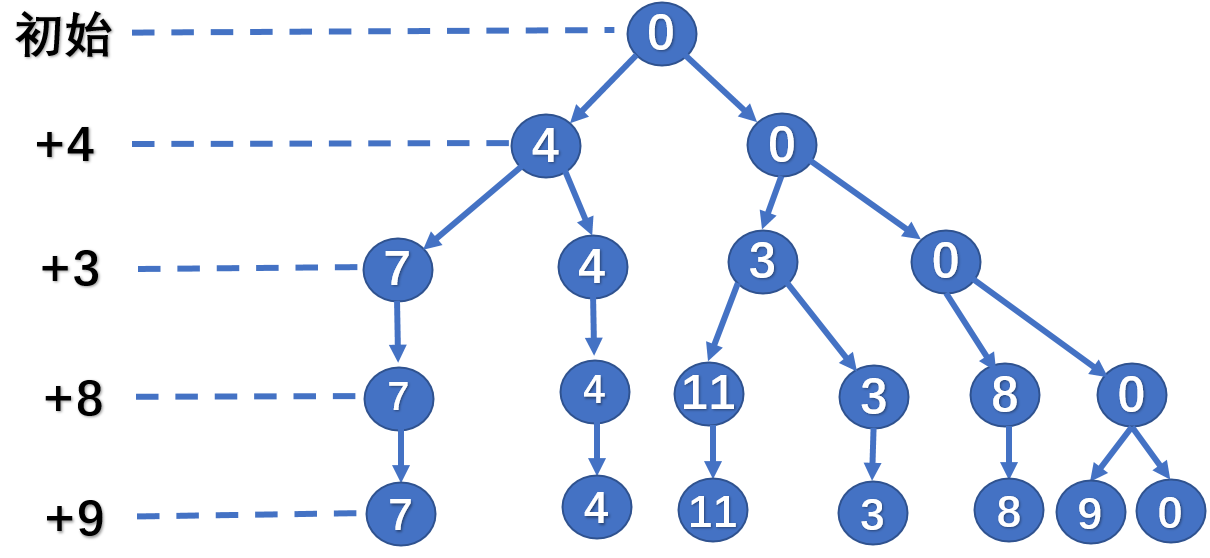
上界计算 先装入物品1,剩余的背包容量为6,只能装入物品2的6/7(即42*(6/7)=36)。 即上界为40+6*6=76
已第一个up为例:40+6*(10-4)=76 打x的部分因为up值已经小于等于bestp了,所以没必要继续递归了。
核心代码 #
- Typew c: 背包容量
- C: 背包容量
- Typew *w: 物品重量数组
- Typew *p: 物品价值数组
- Typew cw:当前重量
- Typew cp:当前价值
- Typep bestcp:当前最优价值
上界函数 #
这和贪心算法有什么区别?
template<class Typew, class Typep>
Typep Knap<Typew, Typep>::Bound(int i)
{// 计算上界
Typew cleft = c - cw; // 剩余容量
Typep b = cp;
// 以剩余物品单位重量价值递减序装入物品
while (i <= n && w[i] <= cleft) {
cleft -= w[i];
b += p[i];
i++;
}
// 装满背包
if (i <= n) b += p[i]/w[i] * cleft;
return b;
}
结点定义 #
static class Bbnode{
BBnode parent; //父结点
boolean leftChild; //左儿子结点标志
…}
static class HeapNode implements Comparable{
BBnode liveNode; //活结点
double upperProfit; //结点的价值上界
double profit; //结点所相应的价值
double weight; //结点所相应的重量
int level; //活结点在子集树中所处的层序号
}
0-1背包问题优先队列分支限界搜索算法 #
6.4 作业分配问题【重点,没看懂】 #
详情参考https://blog.csdn.net/qq_40801709/article/details/90439784
1、问题描述 #
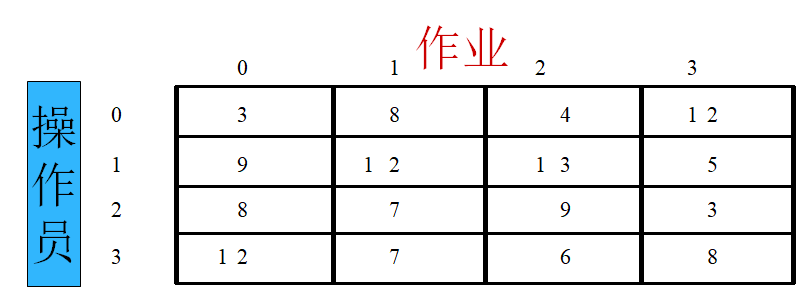
n 个操作员以 n 种不同时间完成 n 种不同作业。要求分配每位操作员完成一项工作,使完成 n 项工作的总时间最少操作员编号为 0,1,…n-1,作业也编号为 0,1,…n-1, 矩阵 c 描述每位操作员完成每个作业时所需的时间,元素 ci,j 表示第 i 位操作员完成第 j 号作业所需的时间 向量 x 描述分配给操作员的作业编号,分量 xi 表示分配给第 i 位操作员的作业编号。
2、思想方法 #
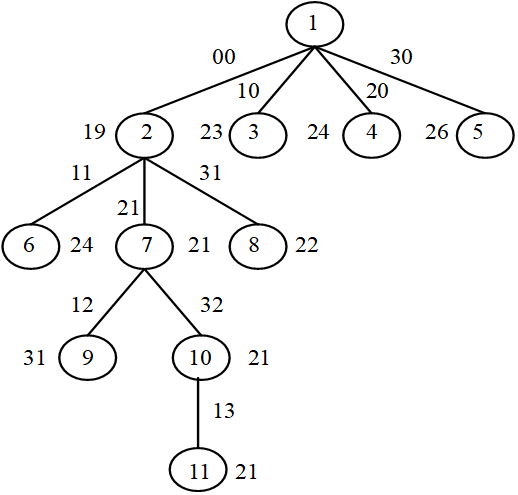
1)从根结点开始,每遇到一个扩展结点,就对它的所有儿子结点计算其下界,把它们登记在结点表中。
2)从表中选取下界最小的结点,重复上述过程。
3)当搜索到一个叶子结点时,如果该结点的下界是结点表中最小的,那么,该结点就是问题的最优解。
4)否则,对下界最小的结点继续进行扩展
3、下界的确认 #
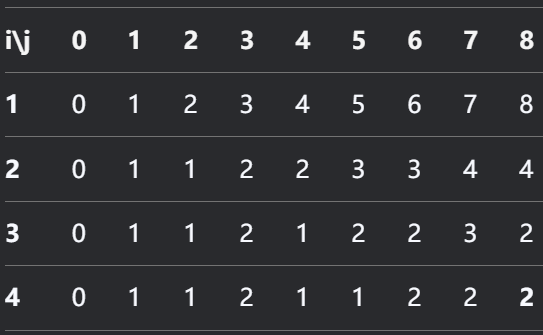
搜索深度为 0 时,把第 0 号作业分配给第 i 位操作员所需时间至少为第 i 位操作员完成第 0 号作业所需时间,加上其余 n-1个作业分别由其余 n-1 位操作员单独完成时所需最短时间之和,有:
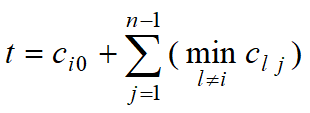
例:4个操作员完成4个作业所需的时间表如下:
把第 0 号作业分配给第 0 位操作员时,所需时间至少不小于 3 + 7 + 6 + 3 = 19 ,把0号作业1 位操作员时,所需 时间至少不会小于9+7+4+3…
搜索深度为 k 时,前面第0,1,……,k-1号作业已分别分配 给编号为i0,i1,……,ik-1的操作员。 S={0,1,……,n-1}表示所有操作员的编号集合;
mk-1={i0,i1,……ik-1}表示作业已分配的操作员编号集合。当把第k号作业分配给编号为ik的操作员时,𝑖𝑘∈𝑆−𝑚𝑘−1, 所需时间至少为:
则上式为把第k号作业分配给编号为ik的操作员时的下界
4、算法实现步骤 #
5、实现代码 #
#include<iostream>
using namespace std;
#define MAX_NUM 99999
const int n = 4;
float c[n][n];//n个操作员分别完成n项作业所需时间
float bound = MAX_NUM;//当前已搜索可行解的最优时间
struct ass_node {
int x[n];//分配给操作员的作业
int k;//搜索深度
float t;//当前搜索深度下,已分配作业所需时间
float b;//本节点所需的时间下界
struct ass_node* next;//优先队列链指针
};
typedef struct ass_node* ASS_NODE;
//把xnode所指向的节点按所需时间下界插入优先队列qbase中,下界越小,优先性越高
void Q_insert(ASS_NODE qbase, ASS_NODE xnode) {
ASS_NODE temp = qbase->next;
ASS_NODE temp2 = qbase;
while (temp != NULL) {
if (xnode->b < temp->b) {
break;
}
temp2 = temp;
temp = temp->next;
}
xnode->next = temp2->next;
temp2->next = xnode;
}
//取下并返回优先队列qbase的首元素
ASS_NODE Q_delete(ASS_NODE qbase) {
//ASS_NODE temp = qbase;
ASS_NODE rt = new ass_node;//只是一个node
if (qbase->next != NULL)
*rt = *qbase->next;
else
rt = NULL;
qbase->next = qbase->next->next;
return rt;
}
//分支限界法实现
float job_assigned(float (*c)[n], int n, int* job) {
int i, j, m;
ASS_NODE xnode,ynode=NULL;
ASS_NODE qbase = new ass_node;
qbase->next = NULL; qbase->b = 0;//空头节点
float min, bound = MAX_NUM;
xnode = new ass_node;
for (i = 0;i < n;i++)
xnode->x[i] = -1;//-1表示尚未分配
xnode->t = xnode->b = 0;
xnode->k = 0;
//非叶子节点,继续向下搜索
while (xnode->k != n) {
//对n个操作员分别判断处理
for (i = 0;i < n;i++) {
if (xnode->x[i] == -1) {//i操作员未分配工作
ynode = new ass_node;//为i操作员建立一个节点
*ynode = *xnode;//把父节点数据复制给它
ynode->x[i] = ynode->k;//作业k分配给操作员i
ynode->t += c[i][ynode->k];//已分配作业累计时间
ynode->b = ynode->t;
ynode->k++;//该节点下一次搜索深度
ynode->next = NULL;
for (j = ynode->k;j < n;j++) {//未分配作业最小时间估计
min = MAX_NUM;
for (m = 0;m < n;m++) {
if ((ynode->x[m] == -1) && c[m][j] < min)
min = c[m][j];
}
ynode->b += min;//本节点所需时间下界
}
if (ynode->b < bound) {
Q_insert(qbase, ynode);//把节点插入优先队列
if (ynode->k == n)//得到一个可行解
bound = ynode->b;//更新可行解的最优下界
}
else delete ynode;//大于可行解最优下界
}
}
delete xnode;//释放节点xnode的缓冲区
xnode = Q_delete(qbase);//取下队列首元素xnode
}
min = xnode->b;
for (i = 0;i < n;i++)//保存最优方案
job[i] = xnode->x[i];
while (qbase->next) {
xnode = Q_delete(qbase);
delete xnode;
}
return min;
}
int main() {
c[0][0] = 3;c[0][1] = 8;c[0][2] = 4;c[0][3] = 12;
c[1][0] = 9;c[1][1] = 12;c[1][2] = 13;c[1][3] = 5;
c[2][0] = 8;c[2][1] = 7;c[2][2] = 9;c[2][3] = 3;
c[3][0] = 12;c[3][1] = 7;c[3][2] = 6;c[3][3] = 8;
int* job = new int[n];
for (int i = 0;i < n;i++)
job[i] = -1;
float result = job_assigned(c, n, job);
for (int i = 0;i < n;i++)
cout << job[i] << " ";
cout << endl;
cout << result << endl;
system("pause");
return 0;
}
近似算法 #

顶点覆盖问题的近似算法 #
VertexSet approxVertexCover ( Graph g ){
cset= 空集
e1=g.e;
while (e1 != null)
从e1中任取一条边(u,v);
cset=cset∪{u,v};
从e1中删去与u和v相关联的所有边;
return cset;
}
过程:
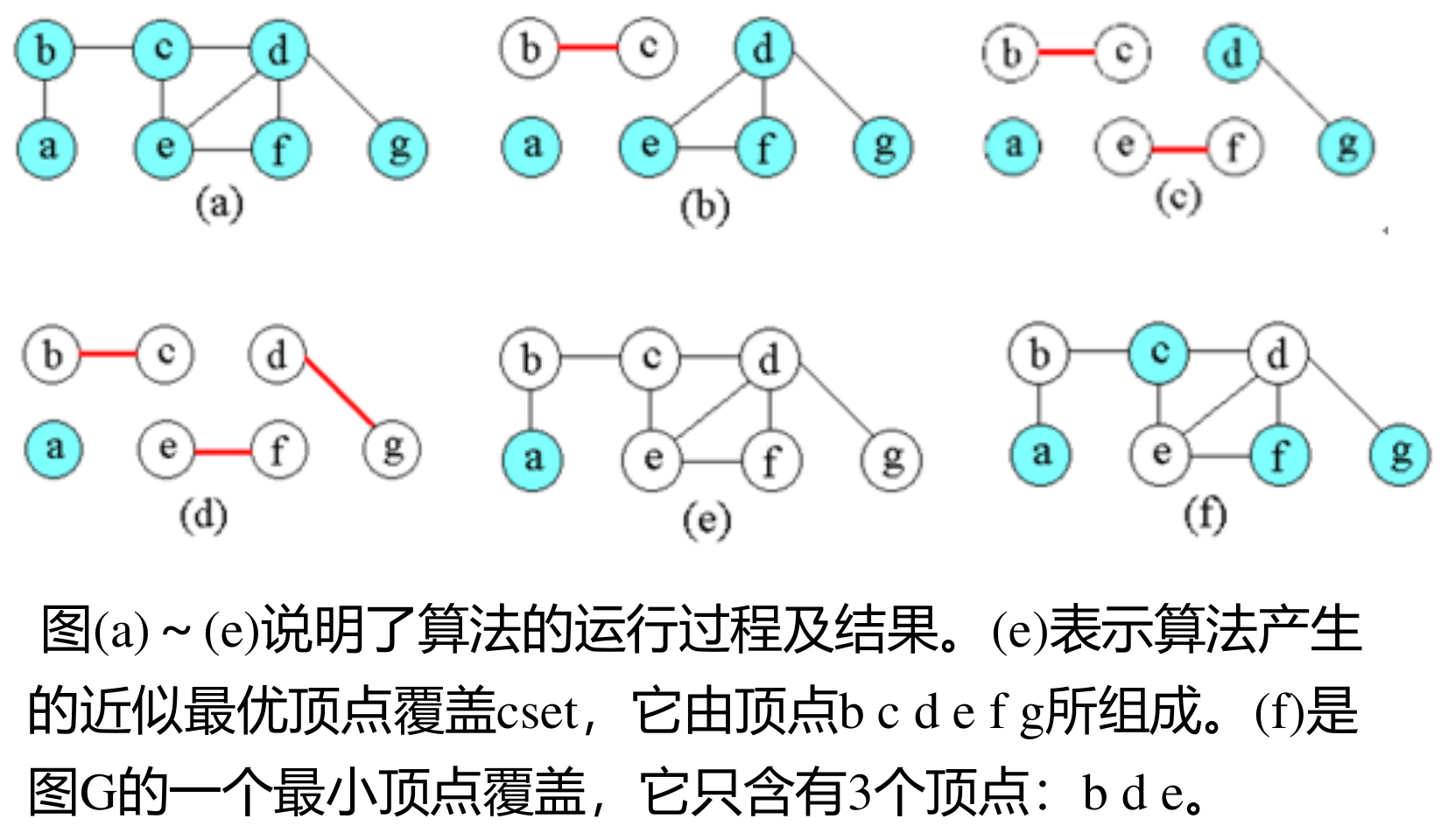
到C的位置的时候,e1中已经没有边了,循环结束。
比较简单的证明,性能比<=2。
◼每条边扫描一次,时间复杂度为O(|E|) ◼Ratio Bound为2。证明如下: ❑令E’为选中的边集,若(u,v)∈ E’,则与其相邻的边都被删除,因此E’中无相邻边; ❑每次选一条边,则每次有两个顶点加入解集A,|A|=2|E’|; ❑设OPT为最优解,由于E’中无邻接边,OPT至少包含E’中每条边的一个顶点,故|E’|≤|OPT|; ❑故|A|=2|E’|≤2|OPT|,从而得性能比 |A|/|OPT|≤2。
一些题目解答 #
1.什么是复杂性和渐进复杂性? 计算资源的量 n趋近于无穷的渐进函数
2.回溯法的约束函数和限界函数是干什么的? 不满足约束条件 不满足最优解
3.最优子结构?

4.什么是算法?
注意16和17的证明。
解决问题的方法或者过程,满足有限性,确定性,可行性。


递归分治1 #
1️⃣第一问
- 第一次:将全体分成9/9/9分别称重,找出较轻的一份
- 第二次:将较轻的一份成3/3/3,找出较轻的一份
- 第三次:将较轻的一份成1/1/1,就此找出轻硬币
2️⃣第二问
- 算法设计:将3𝑘分为3×3𝑘−1后找出较轻者,再将3𝑘−1分为3×3𝑘−2后找出较轻者,递归至最终只有一个硬币
- 递归表达式:𝑇(𝑛)=𝑇(𝑛3)+𝑂(1)
- T ( n ) :原问题的规模
- O ( 1 ) :找出三者中哪个最轻
- T (n3) :分组后需要处理的那1/3份问题的规模
- 复杂度:由主定理直接得𝑛log𝑏𝑎=1与𝑂(1)增长速度一样,所以𝑇(𝑛)=Θ(𝑛log𝑏𝑎log𝑛)=log𝑛
⚠️主定理:𝑇(𝑛)=𝑎𝑇(𝑛𝑏)+𝑓(𝑛),则𝑇(𝑛)有如下渐进界
| 条件 | 结论 |
|---|---|
| f ( n ) 的增长慢于𝑛log𝑏𝑎 | T ( n ) = Θ ( n log b a ) |
| f ( n ) 的增长等于𝑛log𝑏𝑎 | T ( n ) = Θ ( n log b a log n ) |
| f ( n ) 的增长快于𝑛log𝑏𝑎 | T ( n ) = Θ ( f ( n ) ) |
递归分治2 #
int f(int n) {
if (n <= 1) return 1;
return f(n-1)+f(n-2);
}
1️⃣第一问:设𝑓(𝑛)问题中调用了𝑎(𝑛)次𝑓(0),调用了𝑏(𝑛)次𝑓(1)
- 递归条件:
- f ( n ) 本质上就是一堆𝑓(0)/𝑓(1)的相加
- 在𝑓(𝑛)中调用𝑓(0)/𝑓(1)的次数,就是在𝑓(𝑛–1)和𝑓(𝑛–2)中调用𝑓(0)/𝑓(1)的次数的总和
- a ( n ) = a ( n – 1 ) + a ( n – 2 ) 以及𝑏(𝑛)=𝑏(𝑛–1)+𝑏(𝑛–2),二者就是一个斐波那契数列
- 尝试前面几个值:
- f ( 0 ) = 1 直接返回自身的值,算是调用了𝑓(0)一次,所以𝑎(0)=1/𝑏(0)=0
- f ( 1 ) = 1 直接返回自身的值,算是调用了𝑓(1)一次,所以𝑎(1)=0/𝑏(1)=1
- 前两项相加𝑓(2)=2/𝑎(2)=1/𝑏(2)=1
- 前两项相加𝑓(3)=3/𝑎(3)=1/𝑏(3)=2
- 前两项相加𝑓(4)=5/𝑎(4)=2/𝑏(4)=3
- 前两项相加𝑓(5)=8/𝑎(5)=3/𝑏(5)=5
- 可知𝑎(𝑛)比𝑓(𝑛)慢了两步所以𝑎(𝑛)=𝑓(𝑛–2),𝑏(𝑛)比𝑓(𝑛)慢了一步所以𝑏(𝑛)=𝑓(𝑛–1)
2️⃣第二问
- 将规模为𝑛的wenti分解为:规模为𝑛–1的问题+规模为𝑛–2的问题+常数时间合并
- 所以𝑇(𝑛)=𝑇(𝑛–1)+𝑇(𝑛–2)+𝑂(1)
- 这个递归式很难解也不用解,因为题目已经告诉你了𝑓(n)=15((1+52)𝑛+1–(1–52)𝑛+1)
- 所以复杂度为𝑂(𝑓(𝑛))=𝑂(15((1+52)𝑛+1–(1–52)𝑛+1))=𝑂((1+52)𝑛+1)
递归分治3 #
1️⃣算法设计:将𝐴分为两部分,如果A[mid]>mid则查找左半边,如果A[mid]<mid则查找右半边,如此递归
2️⃣复杂度:递归表达式𝑇(𝑛)=𝑇(𝑛2)+𝑂(1),其中𝑂(1)为比较中值大小耗时
- 由此𝑛log𝑏𝑎=1,所以属于主定理的情况二,复杂度为Θ(log𝑛)
1️⃣是什么:给定𝑛种物品和容量为𝐶的背包,物品𝑖的重量为𝑤𝑖价格为𝑣𝑖,如何装物品进去使得背包中物品最贵
- 要求:max∑𝑖=1𝑛𝑣𝑖𝑥𝑖
- 限制:∑𝑖=1𝑛𝑤𝑖𝑥𝑖≤𝐶,其中𝑥𝑖∈0,1用于表示物品𝑖装还是不装,并且1≤𝑖≤𝑛
3️⃣递归结构:𝑚(𝑖,𝑗)=max𝑚(𝑖+1,𝑗–𝑤𝑖)+𝑣𝑖,𝑚(𝑖+1,𝑗)
- j 为当前剩余容量,𝑖表示当前当前正在处理物品𝑖,𝑚是背包已放入物体1→𝑖的价值
- 放入物品𝑖则变为𝑚(𝑖+1,𝑗–𝑤𝑖)+𝑣𝑖,不放入物品𝑖则变为𝑚(𝑖+1,𝑗)
动态规划1 #
1️⃣令(𝑤,𝑣)表示当前背包的<重量,价值>
- 放或不放物品1:
- ( 0 , 0 ) ( 5 , 3 )
- 放或不放物品2:
- ( 0 , 0 ) ( 5 , 3 ) / ( 12 , 4 ) ( 17 , 7 )
- 放或不放物品3:
- ( 0 , 0 ) ( 5 , 3 ) ( 12 , 4 ) ( 17 , 7 ) / ( 6 , 7 ) ( 11 , 10 ) ( 18 , 11 ) ( 23 , 14 )
- 放或不放物品4:
- ( 0 , 0 ) ( 5 , 3 ) ( 12 , 4 ) ( 6 , 7 ) ( 11 , 10 ) / ( 7 , 9 ) ( 12 , 12 ) ( 19 , 13 ) ( 13 , 16 ) ( 18 , 19 )
- 放或不放物品5:新增结点全部被支配,所以无任何变化
- ( 0 , 0 ) ( 5 , 3 ) ( 6 , 7 ) ( 11 , 10 ) ( 7 , 9 ) ( 12 , 12 ) ( 13 , 16 ) ( 18 , 19 )
2️⃣价值最大着(18,19)即为解,对应选择的物品是1/3/4
⚠️注意每一轮需要删掉两种结点
- 一个是总重量大于20的结点
- 另一个是被支配结点,比如结点𝐴的重量比别人大+价值还比别人小,则将其删掉
动态规划2 #
1️⃣第一问
分放或者不放来更新会更加显然一些。
- 放或不放物品1:(2,6)
- 不放:(0,0)
- 放入:(2,6)
- 放或不放物品2:(2,3)
- 不放:(0,0)(2,6)
- 放入:(2,3)(4,9)其中(2,3)被支配
- 放或不放物品3:(6,5)
- 不放:(0,0)(2,6)(4,9)
- 放入:(6,5)(8,11)(10,14)其中(6,5)被支配
- 放或不放物品4:(5,4)
- 不放:(0,0)(2,6)(4,9)(8,11)(10,14)
- 放入:(5,4)(7,10)(9,13)(13,15)(15,18)其中(5,4)被支配
- 放或不放物品5:(4,6)
- 不放:(0,0)(2,6)(4,9)(8,11)(10,14)(7,10)(9,13)(13,15)(15,18)其中(7,10)被支配
- 放入:(4,6)(6,12)(8,15)(12,17)(14,20)(11,16)(13,19)其中(4,6)被支配
2️⃣最优解源于(14,20),选择的是1/2/3/5
动态规划3 #
1️⃣对于数组𝐴,假设以𝐴[𝑖]结尾的子序列长度为𝐿[𝑖]
- 对于介于0→𝑖之间的𝑗,如果𝐴[𝑖]>𝐴[𝑗],则完全可以将𝐴[𝑖]加到以𝑗结尾的子序列当中
- 再与原有的𝐿[𝑖]值比较那个更大,也就是𝐿[𝑖]=max∀𝑗<𝑖𝐿[𝑗]+1,𝐿[𝑖]
- 如果𝐴[𝑖]<𝐴[𝑗]对所有的𝑗成立,则截至到𝐴[𝑗]的升序被打断,𝑖处最大升序只能为1即𝐿[𝑖]=1
2️⃣算法设计
- 设长度𝐿[]=[1]
- 用𝑖遍历𝐴中每个元素
- 用𝑗遍历𝐴[0]到𝐴[𝑖]每个元素
- 如果𝐴[𝑖]>𝐴[𝑗]则𝐿[𝑖]=max𝐿[𝑗]+1,𝐿[𝑖]
- 用𝑗遍历𝐴[0]到𝐴[𝑖]每个元素
- 输出𝐿[]中的最大值
动态规划4 #
https://leetcode.cn/problems/maximum-product-subarray/
1️⃣可能的连续子序列有𝐶𝑛22=𝑂(𝑛2),计算乘的平均长度为𝑛2,所以复杂度为𝑂(𝑛3)或𝑂(𝑛2)(并行优化后)
2️⃣分治法:
- 将𝐴从𝐴[mid]处拆开
- 从𝐴[mid]往最右累乘,计算这一过程中的最大正数𝑅𝑃和最小负数𝑅𝑁
- 从𝐴[mid]往最左累乘,计算这一过程中的最大正数𝐿𝑃和最小负数𝐿𝑁
- 分别计算𝑅𝑃𝐿𝑃/𝑅𝑃𝐿𝑁/𝑅𝑁𝐿𝑃/𝑅𝑁𝐿𝑁,取其中最大值为𝑀
- 将左右两半边按照同样的方式递归处理
- 合并操作:假设每个结点的左/右半边最大乘积为max𝑙/max𝑟,则取maxmax𝑙,max𝑟,𝑀
- 复杂度:假设不论多少位的乘法都可以在𝑂(1)内并行完成,则𝑇(𝑛)=2𝑇(𝑛2)+𝑂(1)
- 说过很多遍了,由主方法可得复杂度为𝑂(𝑛)
3️⃣动态规划:
-
M ( k )的递推:以下分析再加上𝐴[𝑘]自己,𝑀(𝑘)=max𝐴[𝑘],𝑀(𝑘–1)𝐴[𝑘],𝑚(𝑘–1)𝐴[𝑘]
- M ( k ) 潜在的最大:𝐴[𝑘]为负数时,𝑀(𝑘)=𝑚(𝑘–1)𝐴[𝑘]
- M ( k ) 潜在的最大:𝐴[𝑘]为正数时,𝑀(𝑘)=𝑀(𝑘–1)𝐴[𝑘]
-
m ( k )的递推:以下分析再加上𝐴[𝑘]自己,𝑚(𝑘)=min𝐴[𝑘],𝑀(𝑘–1)𝐴[𝑘],𝑚(𝑘–1)𝐴[𝑘]
- m ( k ) 潜在的最小:𝐴[𝑘]为负数时,𝑚(𝑘)=𝑀(𝑘–1)𝐴[𝑘]
- m ( k ) 潜在的最小:𝐴[𝑘]为正数时,𝑚(𝑘)=𝑚(𝑘–1)𝐴[𝑘]
-
算法实现:复杂度为𝑂(𝑛)
-
初始化𝑚[1]=𝐴[0]以及𝑀[1]=𝐴[0]
-
用𝑖遍历整个𝐴数组
- 按照递归式填补𝑚[𝑖]和𝑀[𝑖]
-
输出𝑀[𝑖]最大值
-
代码如下,直接遍历以这个位置结尾的最大值和最小值。
class Solution { public int maxProduct(int[] nums) { int n = nums.length; int[] dpmin = new int[n]; int[] dpmax = new int[n]; dpmin[0] = nums[0]; dpmax[0] = nums[0]; int ans = nums[0]; for(int index = 1; index < n; ++index){ dpmax[index] = Math.max(nums[index], Math.max(dpmax[index - 1] * nums[index], dpmin[index - 1] * nums[index])); dpmin[index] = Math.min(nums[index], Math.min(dpmax[index - 1] * nums[index], dpmin[index - 1] * nums[index])); ans = Math.max(ans, dpmax[index]); } return ans; } }
-
动态规划5 #
1️⃣递推式:对𝑥[𝑖]有两种处理,即使用邮票𝑖或者不使用邮票𝑖
for (int i = 1; i < n; i++) { // 遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
}
}
- 如果不使用:也就是前𝑖–1张以最优结构凑出𝑗,所以𝑐[𝑖][𝑗]=𝑐[𝑖–1][𝑗]
- 如果使用:使用邮票𝑖后构成总邮资𝑗
- 01 背包问题:第𝑖张票不能再用了,也就是要前𝑖–1张邮票再构成总邮资𝑗–𝑥[𝑖]
- 完全背包问题:第𝑖张票有无限个还能再用,也就是要前𝑖张邮票再构成总邮资𝑗–𝑥[𝑖]
- 这里式完全背包问题,所以递归式为𝑐[𝑖][𝑗]=𝑐[𝑖][𝑗–𝑥[𝑖]]+1
- 合起来就是:𝑐[𝑖][𝑗]=min𝑐[𝑖–1][𝑗],𝑐[𝑖][𝑗–𝑥[𝑖]]+1
2️⃣初始条件:
- c [ 1 ] [ j ] :要用第一种邮票构成邮资𝑗,由于𝑥[1]=1,所以𝑐[1][𝑗]=𝑗
- c [ i ] [ 0 ] :要用前𝑖种邮票构成邮资0,什么都不选就行了,所以𝑐[𝑖][0]=0
- c [ i ] [ 1 ] :要用前𝑖种邮票构成邮资1,显然就是选一个𝑥[1]就行了,所以𝑐[𝑖][1]=1
3️⃣四张邮票所以𝑖≤4,最大邮资为8所以𝑗≤8,不断代入递归式就行了
动态规划6 #
1️⃣令𝑠𝑢𝑚[𝑖]为0→𝑖中子段最大和
-
s u m [ i – 1 ]
要么是正数/0
- 为正:为𝑠𝑢𝑚[𝑖]做出正向的贡献,即𝑠𝑢𝑚[𝑖]=𝑠𝑢𝑚[𝑖–1]+𝑎[𝑖]
- 为负:为𝑠𝑢𝑚[𝑖]无贡献,即𝑠𝑢𝑚[𝑖]=𝑎[𝑖]
-
合起来就是:𝑠𝑢𝑚[𝑖]=max𝑠𝑢𝑚[𝑖–1]+𝑎[𝑖],𝑎[𝑖]
3️⃣算法:加上负数抹成0的机制
def max_subarray_sum(a):
if not a:
return 0
dp = [0] * len(a)
dp[0] = a[0]
max_sum = max(dp[0], 0)
for i in range(1, len(a)):
dp[i] = max(dp[i-1] + a[i], a[i])
if dp[i] > max_sum:
max_sum = dp[i]
return max(max_sum, 0)
贪心算法1 #
很奇妙呢,就是直接分成很多的3。
1️⃣这是一个严格的结论:令∀𝑛=3𝑚+r,其中𝑟=𝑛 mod 3
- r =0 是分解为3𝑚
- r =1 是分解为3(𝑚–1)+2+2
- r =2 是分解为3𝑚+2
2️⃣贪心选择性质:算法每一步的局部最优,会带来最终的全局最优
- 首先证明分解数不超过4:假设某一个数分解出现了𝑘≥4,则乘积为𝑘×Rest
- 可以再将𝑘变成𝑘=2+(𝑘–2),则乘积变为了2(𝑘–2)×Rest
- 2 ( k – 2 ) × Rest – k × Rest = ( k – 4 ) × Rest ≥ 0 ,所以消除𝑘能使得乘积更大
- 其次如果选择1也是不行的,比如𝑘×Rest≥1𝑘×Rest
- 所以最优情况必须是划为2或3的总和,接下来需要做的就是判断是以2为主还是以3为主
- 假设选择更多的2为最优,以6为例,<23<32所以不成立
- 所以应该分解为更多的3
- 余数的处理
- 余数为0,不处理
- 余数为1,出现了1就不是最优了,最优的做法是借一个3将其分为2+2
- 余数为2,不处理
贪心算法2 #
0️⃣概念理解
-
X 被𝑌覆盖:也就是𝑋的每个子区间都必须被𝑌的某个子区间覆盖
-
覆盖数:就是𝑌能覆盖𝑋后𝑌有多少子区间
-
也就是中间可以有空的地方,这里要注意一下。
-
注意有一个误区,就是𝑌必须是𝑋的子集,不然一个从头到尾的大区间就覆盖掉了,不论中间有没有空隙
1️⃣贪心策略
- 初始化:将𝑋中第一个区间放入𝑌,作为当前区间
- 更新:重复以下过程
- 如果当前区间与其他区间有交集
- 将选取右边界最大的有交集区间
- 将当前区间与右边界最大的区间进行合并加入到𝑌,形成新的当前区间
- 如果当前区间与其他区间没有交集
- 选取离当前区间距离最小的区间
- 将该区间加入到𝑌中,更新当前区间为该区间
- 如果当前区间与其他区间有交集
2️⃣最优性证明:
- 假设存在某个更优解,其必定在某一部需要选择一个右端点更小的区间
- 从而导致相比原有做法,后续需要更多区间覆盖,不是最优
- 所以矛盾,本方法最优
3️⃣复杂度:只需遍历一次,每个区间在每次遍历时只被处理一次,所以复杂度为𝑂(𝑛)
贪心算法3 #
https://leetcode.cn/problems/assign-cookies/description/
1️⃣首先讲所有小孩/饼干按照饥饿度/饼干大小排序
2️⃣用𝑖指针遍历小孩数组,用𝑗指针遍历饼干数组
- 如果𝐶𝑖>𝐵𝑗,则执行𝑗++
- 如果𝐶𝑖≤𝐵𝑗,则执行𝑗++/𝑖++/Count++
3️⃣最终输出Count
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
int kidsNumber = g.length;
Arrays.sort(s);
int cookiesNumber = s.length;
int ans = 0;
int i = 0;
int j = 0;
while(j < s.length && i < g.length){
if(s[j] >= g[i]){
++i;
++j;
++ans;
}else{
++j;
}
}
return ans;
}
}
回溯法1 #
1️⃣解向量为𝑥1,𝑥2,…,𝑥𝑛其中𝑥𝑖=0/1表示货物𝑖放/不放在船上,约束条件为𝑥𝑖∈0,1和∑𝑖=1𝑤𝑖𝑥𝑖≤𝑐
2️⃣如下图,结点表示当前总重量,遇到结点>120的就剪枝
回溯法2 #
0️⃣𝑛皇后问题:在𝑛×𝑛的棋盘上防止𝑛个皇后,所有的皇后不同行/不同列/不同对角线
- 解向量:𝑥1,𝑥2,…,𝑥𝑛其中𝑥𝑖表示棋子位于第𝑖行第𝑥𝑖列
- 显约束:𝑥𝑖∈1,2,…,𝑛
- 隐约束:𝑥𝑖之间互不相等,不在同一对角线上|𝑥𝑖–𝑥𝑗|≠|𝑖–𝑗|,注意这个是所有对角线
1️⃣解空间树
画个图来直接做剪枝的处理。
回溯法3 #
1️⃣解向量为𝑥1,𝑥2,…,𝑥𝑛,显性约束为𝑥𝑖=0,1,隐约束为∑𝑖=1𝑛𝑥𝑖𝑤𝑖=𝑚
2️⃣解为:8+3
回溯法4 #
1️⃣解向量为𝑥1,𝑥2,…,𝑥𝑛
-
显约束为𝑥𝑛=1,2,…,𝑛且互相间不相同
-
隐约束为在解向量中,当前在栈中的元素,必定排在已出栈元素的后面
-
开始输出之后,就要一次性全部都输出出去。
2️⃣123进栈后能输出的只有:123/132/213/321,完全倒推出解空间树
回溯法5(递归回溯) #
0️⃣注意这个问题进行的是深度优先搜索,即递归回溯,具体的图我就不画了
1️⃣算法思路:假设有𝑛个结点时
- 初始化当前最优为1→2→3→4→5→1的距离,以便快速收敛
- 回溯函数:用𝑖遍历树的每层:
- 当𝑖<𝑛时,尝试将其与除结点𝑖外的下一层结点进行连接,如果从根到下一节点路径长于最优,则剪枝
- 当𝑖=𝑛时,尝试与起始点进行连接,如果能与起始点连接则计算哈密顿路径,更小则更新最优值
- 输出最终的最优值 0
NP1 #
**(稠密子图问题DEN-SG)**给定无向图G,判定G中是否存在一个子图H,它有k个顶点,且至少有y条边。已知k团问题CLIQUE是NP完全问题,请证明稠密子图问题DEN-SG是NP完全问题。
1️⃣两个问题分别是什么
- 稠密子图问题:给定无向图𝐺,要寻找它的一个包含𝑘个顶点的子图,并且该子图边数大于等于𝑦
- 团问题:给定无向图𝐺,要寻找它的一个包含𝑘个顶点的子图,并且该子图结点互相两两连接
2️⃣先证明稠密子图NP,即它可在多项式时间内验证
- 遍历子图所有顶点,并计算其边数,即可判断其总边数是否大于𝑦
- 耗𝑂(𝑘2),所以是NP问题
3️⃣证明团问题可以线性时间内规约到稠密子图问题
很显然的直接推理就可以。
- 构建团问题的实例(𝐺,𝑘):图𝐺中存在𝑘个结点两两连接的子图,则子图中边数为𝑘(𝑘−1)2
- 构建稠密子图问题的实例(𝐺,𝑘,𝑘(𝑘−1)2)
- 当团实例成立时,该稠密子图实例也成立,故团问题在多项式时间内规约到了稠密子图问题,证毕
NP2 #
证明顶点覆盖问题(Vertex Cover Problem)属于NPC类
1️⃣两个问题分别是什么
- 顶点覆盖问题:给定无向图𝐺,要寻找它的一个包含𝑘个顶点的子图,子图所有点能连接到图中所有边
- 团问题:给定无向图𝐺,要寻找它的一个包含𝑘个顶点的子图,并且该子图结点互相两两连接
2️⃣证明顶点覆盖问题是NP:也就是可在所想是时间内验证
- 遍历子图中每一个点,记录每一点所连接的边,最后看这些边是否覆盖了所有边
- 时间复杂度𝑂(𝑘2)
3️⃣证明团问题可以线性时间内规约到顶点覆盖问题
- 构建一个团问题的实例(𝐺,𝑘):图𝐺中存在𝑘个结点两两连接的子图
- 构建覆盖问题实例(𝐺,|𝐺|−𝑘)
- 由于定理可知,当团问题实例成立时,覆盖问题实例也一定成立,证毕
NP3 #
1️⃣证明子集覆盖时NP的:遍历𝐶中每一子集,从左到右依次合并,将最终结果与𝑋对比,即可在𝑂(𝑛)内验证
2️⃣证明顶点覆盖问题可在多项式时间内规约到子集覆盖问题
核心的思路就是,全集为所有边,一个点关联的所有边为一个子集
子图中点的边全覆盖了所有边,变成了子图中点对应的边的子集覆盖了全集
NP4 #
👉𝑃问题:可在多项式时间内求解
👉𝑁𝑃问题:可在多项式时间内验证,但无法求解
👉𝑁𝑃𝐶问题:最难的𝑁𝑃问题
👉𝑁𝑃难问题:难度比𝑁𝑃𝐶还要难的问题,但不一定是𝑁𝑃问题
1️⃣分别对/错/错,见上图
(判断)若问题A是一个P类问题,则A也是一个NP类问题 (判断)所有NP难问题都是NP问题 (判断)若问题A是一个NP问题,则A也是一P类问题
➡️由上图可知,选D
2️⃣不对,不是上界是下界
注意:在A归约B的情况下,到A的下界推出B的下界(相减),B的上界推出A的上界(相加)。
(判断)若问题A的计算时间上界为O(𝑛2),且问题A可在O(n)时间内变换为问题B,则问题B的计算时间上界也O(𝑛2)
- 记住NP问题规约的一些结论:若𝐴可在𝑂(𝜏(𝑛))时间内变换到𝐵,即𝐴∝𝜏(𝑛)𝐵
- 显然凭直觉有𝑇𝐴=𝑂(𝜏(𝑛))+𝑇𝐵
- 则𝑇𝐴−𝑂(𝜏(𝑛))为𝐵的下界
- 则𝑇𝐵+𝑂(𝜏(𝑛))为𝐴的上界
➡️由以上结论可得选𝐷
3️⃣选𝐵要记住,如果𝐴是𝑁𝑃𝐶+𝐵是𝑁𝑃+𝐴线性时间可转化为𝐵,则𝐵是𝑁𝑃𝐶
算法导论 #
1️⃣不对,程序可以无限执行,比如系统进程
(判断)算法和程序都必须满足有限性,即在执行有限时间后结束
2️⃣两个都对
(判断)若f(n)=O(g(n)),且f(n)=Ω(g(n)),则f(n)=Θ(g(n))
(判断)若f(n)=Θ(g(n)),则f(n)=Ω(g(n))
- f ( n ) = O ( g ( n ) ) 即𝑓(𝑛)≤𝑐1𝑔(𝑛),𝑓(𝑛)=Ω(𝑔(𝑛))即𝑓(𝑛)≥𝑐2𝑔(𝑛),于是𝑐2𝑔(𝑛)≤𝑓(𝑛)≤𝑐1𝑔(𝑛)这就是𝛩(𝑔(𝑛))的定义
- Θ ( g ( n ) ) 即𝑐2𝑔(𝑛)≤𝑓(𝑛)≤𝑐1𝑔(𝑛),于是𝑐2𝑔(𝑛)≤𝑓(𝑛)这就是Ω(𝑔(𝑛))的定义
3️⃣就是说𝑓的增长要快于𝑔,所以是大于等于,也就是不小于,选𝐵
➡️即𝑓(𝑛)≤𝑐𝑔(𝑛),说明𝑔(𝑛)增长更快,所以𝑓(𝑛)阶更小(小于等于),选𝐴
➡️最好情况是紧的𝑐𝑓(𝑛),所以平均情况肯定要高于𝑐𝑓(𝑛),也就是以𝑐𝑓(𝑛)为下界,也就是Ω(𝑓(𝑛))选B
4️⃣(7×2𝑛)×2=7×2𝑛′所以𝑛′=𝑛+1选𝐴
➡️错误,归并排序又不是𝑂(𝑛)的
如果一个归并排序算法在某台机器上用1秒钟排序5000个记录,则用2秒钟可以排序10000个记录
递归分治 #
1️⃣不对,直接间接调用,一个不能少
(判断)递归算法就是指一个直接调用自身的算法。
2️⃣对的,不断将问题分治为更小的规模
(判断)二分法搜索算法是运用了分治策略设计的。
3️⃣不对,也可以分治后,循环遍历处理每个子问题
分治必须用递归实现
4️⃣由主定理可知𝑛log𝑏𝑎=𝑛,属于情况1,所以为Θ(𝑛log𝑏𝑎)=Θ(𝑛),选𝐵
主定理:𝑇(𝑛)=𝑎𝑇(𝑛𝑏)+𝑓(𝑛),则𝑇(𝑛)有如下渐进界
| 条件 | 结论 |
|---|---|
| f ( n ) 的增长慢于𝑛log𝑏𝑎 | T ( n ) = Θ ( n log b a ) |
| f ( n ) 的增长等于𝑛log𝑏𝑎 | T ( n ) = Θ ( n log b a log n ) |
| f ( n ) 的增长快于𝑛log𝑏𝑎 | T ( n ) = Θ ( f ( n ) ) |
➡️采用的分治法,一分为二,左右两边都要处理,所以𝑇(𝑛)=2𝑇(𝑛2)+𝑐,所以是Θ(𝑛)
5️⃣分别是:分治,贪心( Dijkstra ),动态规划,贪心。所以选A
贪心 #
1️⃣非01背包就是要价值/背包中总重最大,所以也一定是贪心地做出最有利于增大这一比例的选择
- 但是注意这里的非01背包问题,区别于01背包问题,可以将每个物品分割后放入
2️⃣选𝐶,每次贪心地选择一行内总和最小的两个数
3️⃣贪心( Dijkstra ),因为每次都选离当前结点最近的点
4️⃣都对,详见下
(判断)在求最小生成树的算法中, Kruskal算法使用的是贪心策略
(判断)求最小生成树的Prim算法使用的设计策略是贪心策略
- Kruskal :边扩展,操作对象为所有边,选择权重最小的边加入生成树中
- Prim :点扩展,操作对象为与当前生成树连接的边,选择权重最小边的点加入生成树中
DP #
1️⃣不对,动态规划适用于解决最优子结构+重叠子问题的确定性问题
(判断)动态规划适合求解动态不确定性问题。
2️⃣对的,这是定义
(判断)最优子结构性质是指问题的最优解包含了子问题的最优解。
3️⃣选𝐵,这是定义
4️⃣不对,详见下表
(判断)动态规划算法与分治法都采用自底向上的计算方式
| 特性 | 动态规划 | 分治法 |
|---|---|---|
| 分解方式 | 子问题可能重叠 | 子问题相互独立 |
| 计算方向 | 自底向上 | 自顶向下 |
| 是否存储子问题解 | 需要存储子问题解以避免重复计算 | 不需要存储子问题解 |
回溯算法 #
1️⃣正确:区别见下
(判断)回溯法和分支限界法都是在问题解空间树上搜索问题解的算法
- 搜索策略不同:回溯法通常采用深度优先搜索,而分支限界法通常采用广度优先或最小耗费优先搜索
- 剪枝方式不同:回溯法主要依赖约束条件,而分支限界法依赖限界函数
2️⃣选𝐴,基本概念
3️⃣选𝐶,回溯法是用约束条件剪去不满足约束的点及其子树,分支界限使用限界函数减去得不到最优解的子树
4️⃣最坏情况要遍历所有的叶节点,有多少种排列就有几个叶节点,排列数为𝑛!,所以复杂度为𝑂(𝑛!)
分支限界 #
1️⃣选𝐷,我们上面之前讲得比较清楚了
2️⃣选𝐵,分析见下
- 首先了解这三个概念
- 活结点:本身已生成,子节点还未全部生成
- 扩展结点:正在生成子节点
- 死结点:子节点全部生成完毕
- 回溯法:深度优先
- 比如当前结点有多个子节点,当前生成了一个结点后,先往深处搜索
- 搜索到底部了之后,再回溯过来生成下一个子节点
- 所有有多次机会
- 分支界限法:广度优先,一次性一股脑生成所有子节点,所以只有一次机会
3️⃣对的,结点选择方法,比如栈式分支/队列式分支/优先对列分支,会影响搜索的路径和效率
(判断)扩展节点的选择影响分支限界法
4️⃣不对,二者的根本差别不在用不用栈,而在深度优先和广度优先搜索,还有剪枝规则
(判断)在分支限界法中,如果将活结点用栈来存储,则这种分支界限法就是回溯法
概念题目 #
1️⃣写出分治、动态规划、贪心、回溯算法的策略
- 分治:自上而下地将一个复杂问题分为若干简单可直接求解的子问题,通过子问题的解得到原有问题的解
- 动态规划:将原问题分为互相重叠的子问题,分别解决子问题最终自下而上地合并为原问题的解
- 贪心:每一步都采取当前状态下最好的选择,从而导致全局都是最优的
- 回溯:在问题的解空间树上深度优先搜索问题的解,并在不满足约束条件时进行剪枝回退
2️⃣什么是算法的复杂性? 什么是算法的渐进复杂性?
- 复杂性:算法运行所需要的所有计算资源
- 渐进复杂度:算法规模趋近于穷时,算法的复杂性所趋近的值
3️⃣在回溯法中, 什么是约束函数和界限函数? 它们在搜索过程中的作用是什么?
- 约束函数:用于检测是否满足约束条件,用于在回溯法中剪去不满足约束条件的结点及其子树
- 界限函数:用于计算当前结点是否能达到最优,用于剪去不能达到最优的结点及其子树
4️⃣什么是最优子结构? 请举例说明。
- 最优子结构:当一个问题的最优解包含其所有子问题的最优解时,称之为具有最优子结构
- 比如:Dijkstra问题中最短路径就具有最优子结构
5️⃣线性时间选择算法:找到第𝑘小的数
- 将输入数组按5个一组划分,每组内元素进行排序,选出每组中位数组成一个新的数组
- 对新数组再进行相同操作,得到中位数的中位数,作为数组的Pivot划分数组
- 确定第𝑘小的数在数组那一部分,然后递归地处理呢一部分
6️⃣什么是算法?算法应满足的标准是什么?
- 算法:解决问题的方法和过程,有穷操作和指令的集合
- 标准:确定性,有穷性,可行性,健壮性