Table of Contents

CSAPP:CacheLab
#

本次lab分为A和B两部分，我先看情况做，并且会部分引用我校助教撰写的一些内容以及思考题，首先我们要熟悉一下Cache的工作原理，关于这一部分的内容，你也可以看我的ComputerOrgnization中的内容（写的不怎么样，你最好还是看课本，而且我还建议你做一下课本上的习题），A部分是实现一个3级Cache，实现的过程中我们应当会对Cache的工作原理更加熟悉，B部分是优化矩阵转置函数，我认为会教会我们什么是Cahce友好的代码。

注意：以下不会从零开始讲述Cache的知识，并且不要抄袭，不要抄袭，不要抄袭。

Cache:计算机的世界无处不在的伟大思想……

熟悉：

CacheLine的组织方式
#

可以看成是一个元素是CacheLine的二维数组。

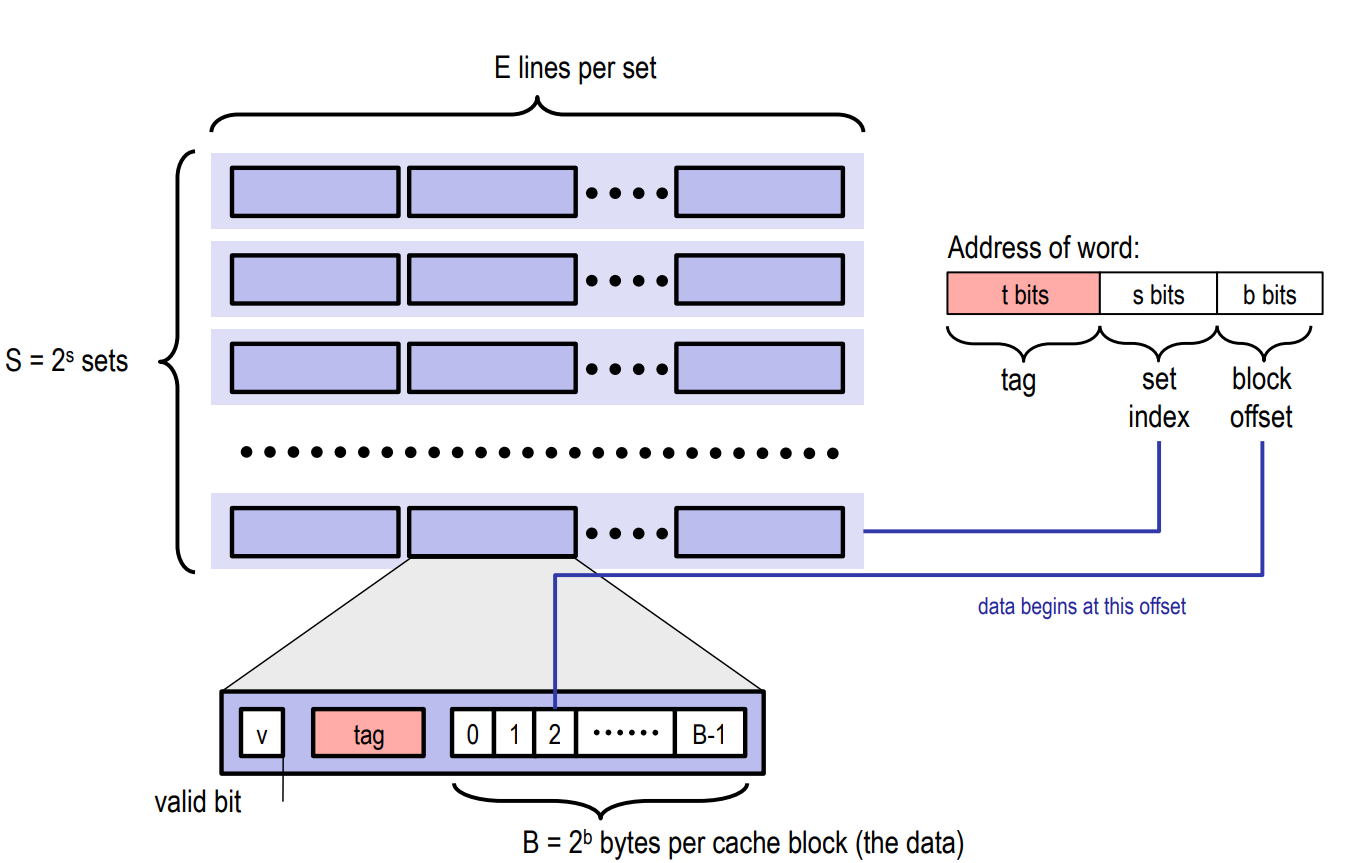
https://xjtu-ics.github.io/assets/images/cachelab_memory_orgnization.png

E = 1:直接映射

S = 1：全相联映射

处理写操作的方法
#

cache处理写操作的流程比读取要复杂，因为写入操作涉及数据的更改，一旦涉及修改操作，就会带来各种一致性问题，因此cache需要合理的处理数据更改的时机和范围。同时还需要处理写miss的情况。我们在这里简要介绍一下有关写cache的一些问题和处理机制。

一般而言，对于写入操作，cache一般有两种处理机制，分别是：

write back（写回）：即数据的修改只发生在当前这一级cache中，通常会引入一个dirty标记位，表示cache中的数据和下一级cache（或内存）中的数据不一致，只有在当前的cacheline被evict的时候才会将数据写回到下一级cache（或内存）。
write through（写直达）：顾名思义，写入操作会同时将数据写入到当前cache和下一级cache（或内存中），因此二者的数据是同步的。

除了上述的两种策略，cache还需要确定如何处理write miss的情况，一般而言，也有两种方法：

write allocate（写分配）：当发生cache miss时，需要访问下一级cache（或内存）将需要的cache line加载到当前cache中，然后再修改这个cache line中的内容
no write allocate（写不分配）：当发生cache miss时，无需修改当前cache中的内容，直接写入下一级cache（或内存）

上述策略两两组合可以产生4种不同的写策略，但是一般常见的只有以下两种：

write back/write allocate：即写回+写分配策略（图片来自wiki）

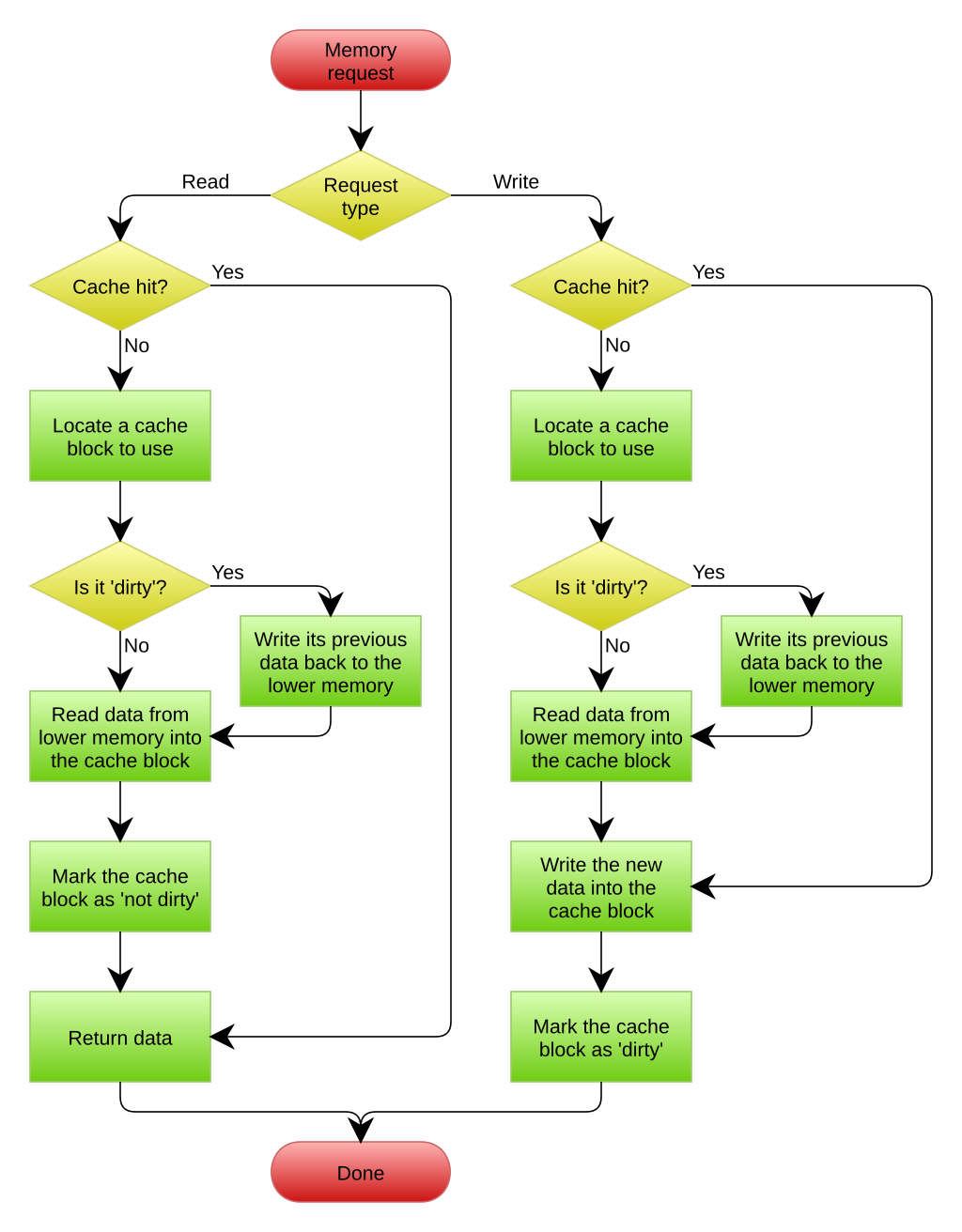
write through/no write allocate：即写直达+写不分配策略

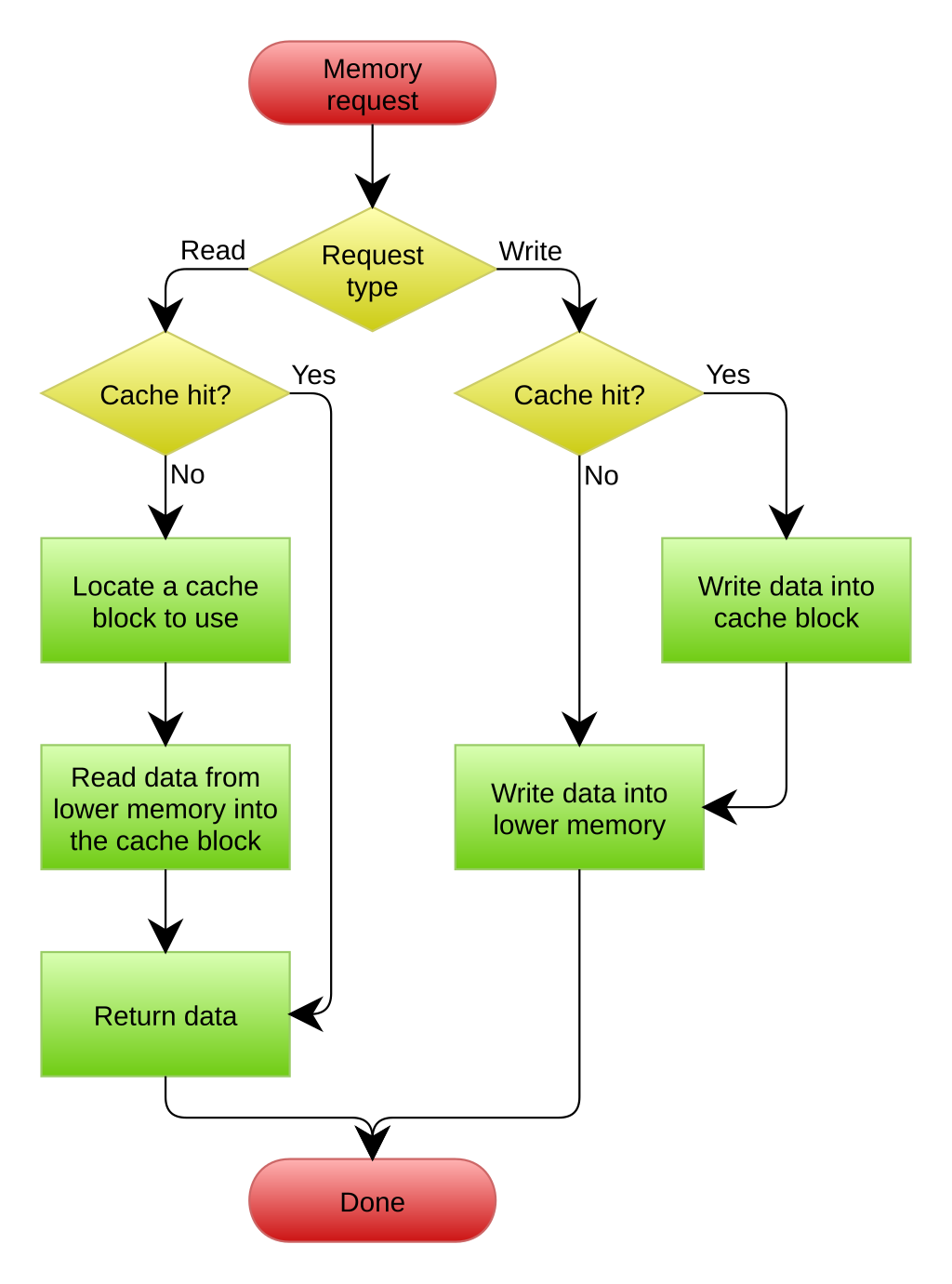
Q：为什么没有写回和写不分配的操作？

A：试想一下这样的情况：有二级缓存L1和L2,我们在L1写某个内存时发生了CacheMiss，假如我们写这个的概率很高，那么这块内存应该加载到L1才更加合理，但是每次都会发生CacheMiss，这不符合时间局部性的要求。另外一种方式也可以这样思考一下。

多级cache的包含准则(inclusion policy)
#

这是本Lab的重中之重，请务必仔细理解。

包含性策略：更高层次的，访问速度更快的cache包含的内容是下层cache的一个子集。

现代处理器中的 L1 和 L2 Cache 可能采用不同的 一致性策略，主要有：

包容式（Inclusive）Cache：L2 必须包含 L1 中的所有数据。
非包容式（Non-Inclusive）Cache：L1 和 L2 不必强制包含相同数据，可以各自缓存不同的数据。
独占式（Exclusive）Cache：L1 和 L2 不共享数据，数据只存在一个层级。

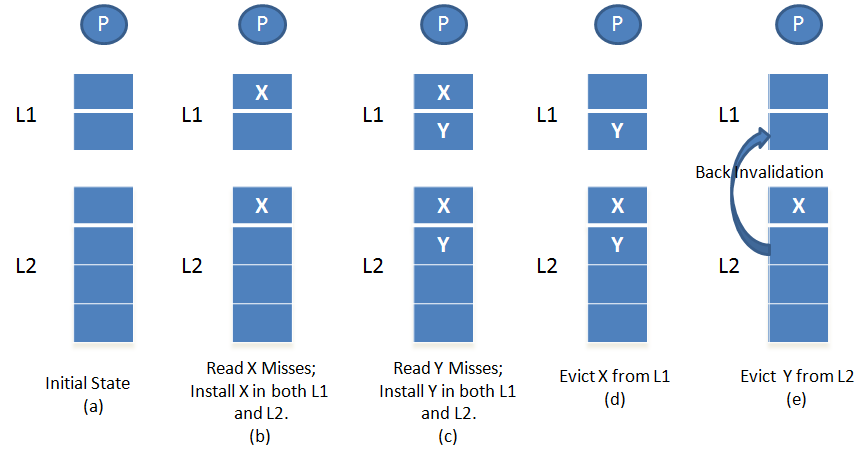
https://xjtu-ics.github.io/assets/images/Inclusive.png

如上图的一个模拟情况：

多余不再赘述，我们只需要注意这样两点：

1.上层的存储不断Cache Miss时，直到找到没有Cache Miss的这样一层，接着要把这个数据加载到之前Cache Miss的每一层。

2.当下层的存储发生Cache Evict时，我们要把这一层之上的所有这个数据置为无效，显然，对于Inclusive Policy，如果不驱逐就不满足子集条件。

三级Cache模拟器
#

我们要实现这样一个Cache：

https://xjtu-ics.github.io/assets/images/three_level_cache.png

L1分为L1D（数据读写）和L1I（指令读取）两个分离的cache，并且L1I是只读的。
L1和L2为每个核心私有
L2为unfied cache，也就是会同时存储指令和数据
L3为unfied cache，且所有核心共享

每个Cache的具体配置，方便查阅：

每个cache的具体配置如下：
- L1D(I) cache
  - size: 64B
  - set: 4
  - associativity: 2-way
  - cache line size: 8B
  - write policy: write back + write allocate
- L2 cache
  - size: 256B
  - set: 8
  - associativity: 4-way
  - cache line size: 8B
  - write poliy: write back + write allocate
  - inclusion policy: inclusive
- L3 cache
  - size: 2KB
  - set: 16
  - associativity: 8-way
  - cache line size: 16B
  - write policy: write back + write allocate
  - inclusion policy: inclusive

我们实现单核的CPU中的缓存机制，不考虑并发访问和与核心的缓存一致性问题。

小小吐槽一下：我们学校的助教简直已经把lab喂到嘴里了，把一整个lab变成了leetcode一样的核心代码模式，这样不好，但是门槛会变低。

（对不起，误会了，还是挺难的……）

先读一下定义的头文件：

/*
 * cachelab.h - Prototypes for Cache Lab helper functions
 */

#ifndef CACHE_LAB_H
#define CACHE_LAB_H

#include <stdbool.h>
#include <stdint.h>

#define L1_SET_NUM 4
#define L1_LINE_NUM 2
#define L1_CACHELINE_SIZE 8

#define L2_SET_NUM 8
#define L2_LINE_NUM 4
#define L2_CACHELINE_SIZE 8

#define L3_SET_NUM 16
#define L3_LINE_NUM 8
#define L3_CACHELINE_SIZE 16

#define ADDRESS_LENGTH 64

#define MAX_TRANS_FUNCS 100

//核心的CacheLine是一个结构体
typedef struct {
  bool valid;
  bool dirty;
  uint64_t tag;
  uint64_t latest_used; // for LRU
} CacheLine;

typedef struct trans_func {
  void (*func_ptr)(int M, int N, int[N][M], int[M][N]);
  char *description;
  char correct;
  unsigned int num_hits;
  unsigned int num_misses;
  unsigned int num_evictions;
} trans_func_t;

// defined in csim.c
extern CacheLine l1dcache[L1_SET_NUM][L1_LINE_NUM];
// L1 Instruction Cache
extern CacheLine l1icache[L1_SET_NUM][L1_LINE_NUM];
// L2 Unified Cache
extern CacheLine l2ucache[L2_SET_NUM][L2_LINE_NUM];
// L2 Unified Cache
extern CacheLine l3ucache[L3_SET_NUM][L3_LINE_NUM];

/* Fill the matrix with data */
void initMatrix(int M, int N, int A[N][M], int B[M][N]);

/* The baseline trans function that produces correct results. */
void correctTrans(int M, int N, int A[N][M], int B[M][N]);

/* Add the given function to the function list */
void registerTransFunction(void (*trans)(int M, int N, int[N][M], int[M][N]),
                           char *desc);

#endif

实现的时候我们按照如下的顺序（程序框图,假设我们在访问第i级Cache）：

根据内存地址得到相应的tag，set字段的值
检查第 i 级cache是否命中
如果命中，跳到第8步
否则，继续访问下一级cache（或内存）获取数据
在本级cache对应的set中找一个invalid的cache line，用于放置从下一级cache（或内存）加载的cache line，如果有多个invalid的cache line，选择下标最小的一个，然后跳到第8步
如果在第5步对应的set已满，你需要首先evict一个cache line，evict的过程使用LRU算法，如果evict的cache line是dirty的，你需要首先将其写入到下一级缓存（或内存）
由于inclusive policy，你可能需要back invalidation第 i - 1 级cache中的cache line
设置这个cache line对应的tag字段，LRU字段和valid字段
如果访问模式是写操作，设置dirty字段
返回

给了我们一个例子，我来看看……

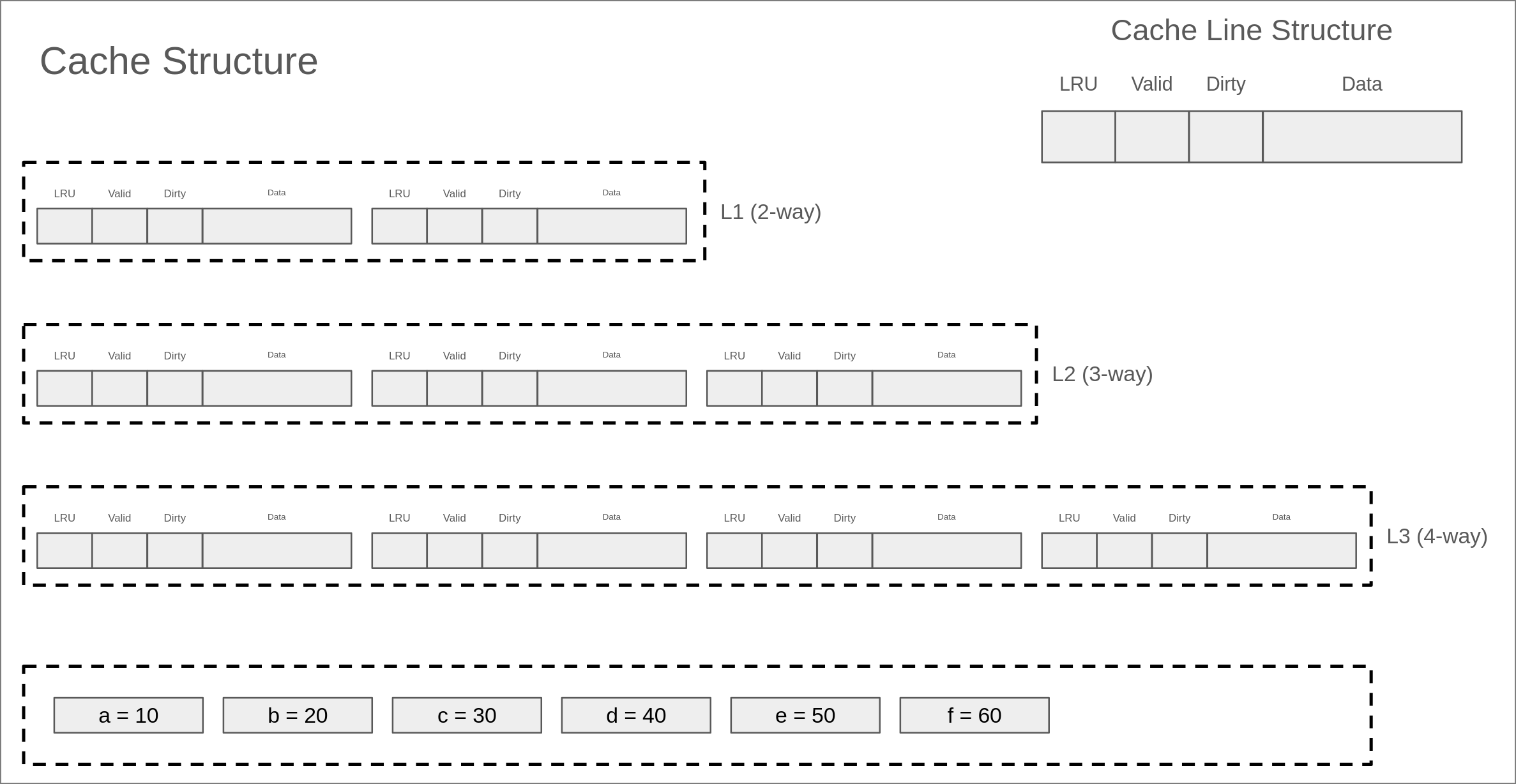
https://xjtu-ics.github.io/assets/images/cache_sim.png

cache的访问trace依次为：

Read a
Read b
Read a
Write b
Read c
Write a
Read d
Read c
Write b
Write c
Read e
Read f
Read b
Read d

画一画吧，这个还是挺复杂的，最复杂的地方就在于驱逐的时候Back Invalidation的逻辑。

助教给出的一些注意事项：

在访问cache之前，你需要正确的初始化所有的cache line, 换句话说，你需要把所有的字段全部初始化为0

你可以假设，对于单个cache的访问，不会出现跨两个cache line的情况，换句话说，你可以忽略cacheAccess函数中的第三个参数

对于M类型的访问，你可以等价的将他看作为一次读取和一次写入

需要注意的是，L2和L3 cache会同时包含指令和数据

你可以假设指令和数据不会访问同一块内存，换句话说，你可以假设L2中的某个cache line不会同时出现在L1D cache和L1I cache中

这里TMD是这样的么，我假设访问一块内存之后就过了一堆样例（也有可能是我误人子弟了。。。。。。）

本次实验仅要求模拟cache访问，因此你无需关心具体的写入数据

你可以使用位运算相关技巧从传入的地址中提取出tag，set，block等信息

你可以使用位运算相关技巧根据tag，set，block的信息拼接出内存地址

在加载一条cache line时，你需要在当前cache set中找出一条可用的cache line, 换句话说，你需要找到一条valid字段为false的cache line。如果有多条可用的cache line，你需要选择下标最小的一个

你需要严格使用LRU算法来找到需要evict的cache line

你可以简单使用循环的方式来暴力实现LRU，而不考虑复杂度的问题，为此，你可以维护一个全局时钟并且仔细的设置cache line结构中的latest_used字段

在evict一条cache line时，你需要考虑dirty字段的影响，换句话说，如果dirty为true，你需要在加载新的cache line之前，将旧的cache line写回到下一级cache（或内存）。如果dirty为false，你可以简单的将这条cache line丢弃

你在进行evict的时候，无需对evict的cache line的LRU字段进行改动

你需要在每次成功访问一条cache line之后设置LRU字段，成功访问指写入/读取命中，或者是从下级缓存加载了相应的cache line之后的读取/写入操作

在发生conflict miss时，你需要严格遵守先fetch，后evict的过程，即先访问下一级缓存或者内存得到数据所在的cache line，再选择需要evict的cache line，这可能会影响LRU设置的顺序。考虑一个例子，假如某个时刻全局时钟为10，L1发生conflict miss，L2 hit，你需要首先访问L2，由于L2 hit，设置L2中对应的cache line的LRU为10，然后将cache line返回给L1，假设L1需要evict的cache line是dirty的，你需要将其首先写回L2，这是100% hit的（为什么？），因此设置L2中对应的cache line的LRU为11，最后将需要的cache line放置在L1经evict空出的位置上，然后设置对应的LRU为12

本次实验要求上一级cache的内容一定存在于下一级cache中，这叫做inclusive policy。你需要时刻保证这一条性质，并且好好利用它

受限于inclusive policy，写回脏数据的过程实际上是100% hit的，你需要合理的安排代码顺序实现这一点

当你处理write miss时，需要首先访问下一级缓存（或者内存）获取cache line，然后再写入这条cache line。在此过程中，你需要仔细思考对于下一级缓存应该以什么类型进行访问

如果你需要从L2 evict某个cache line，假设这个cache line也存在于L1, 你需要将L1中对应的cache line也进行evict，这个过程叫做back invalidation。如果L1中的数据是dirty的，你需要首先将其写回L2。

如果你需要从L3 evict一个cache line，你也需要分别将L1和L2中对应的cache line进行evict。在此过程中，你需要好好思考evict的顺序，以保证inclusive的性质。

注意，不同级别的缓存cache line的大小可能是不一样，你在设计代码的时候需要考虑这会产生哪些影响，并仔细的处理相关流程

vscode ctrl + shift + I整理代码

我草，debug快疯了……（debug日记）

//分析一下错误
Testcase                                     Lines     Result    Random    Score     
---------------------------------------------------------------------------------
traces-data-intensive/long.trace             267988    FAIL      IGNORE    0/3       
  Details for trace <traces-data-intensive/long.trace>
                          Your simulator           Reference simulator
     Level      Hits    Misses    Evicts      Hits    Misses    Evicts
      L1 D    231249     55715     53833    230444     56520     53285
      L1 I         0         0         0         0         0         0
        L2     46998     26645     26424     47391     27797     24629
        L3     32061     10181     10053     33435     11645     11517

hits 和 misses的和相等，但是差刚好差了805,hits多了，misses少了，随之evict也会变多，这应该不是计数而是逻辑的问题

races-basic/mixed-2.trace                   90        FAIL      IGNORE    0/5       
  Details for trace <traces-basic/mixed-2.trace>
                          Your simulator           Reference simulator
     Level      Hits    Misses    Evicts      Hits    Misses    Evicts
      L1 D        20        60        52        20        60        52
      L1 I        18        12         7        17        13         6
        L2        71        43        15        71        44        16
        L3        19        28         0        21        28         0

为什么I指令自己没错，分开都没错，但是结合到一起就出错了,两者之间为什么会相互影响？？？

traces-hard/grep.trace                       406467    FAIL      IGNORE    0/1       
  Details for trace <traces-hard/grep.trace>
                          Your simulator           Reference simulator
     Level      Hits    Misses    Evicts      Hits    Misses    Evicts
      L1 D     37304      1068       949     22544     15828       502
      L1 I    184075    184064    184034    184075    184064    184016
        L2    176099      9087      9055    118023     81983     81951
        L3      6693      2413      2285     79669      2416      2288

L3hits之间差距过大,L2中的数据没有及时驱逐？？？

先放这，休息一下再看。

已经拿了76分，但实在是很难找到剩下的逻辑错误！煎熬！

OK，最后拿了93分，差一点点实在是找不出来为啥了,不贴源代码了，写了六七百行能跑的垃圾，之后再精简总结一下,这下是真尽力了，我感觉已经不是一个设计的问题了，到最后我甚至要去猜哪里的设计提示是不是说的有问题，有错误，那就没有意思了对么……

最后应该是因为三层地址中block位并不一样的原因，这里要细节处理一下，因为你直接把L3的block干成0,可能会对于L2的setIndex位产生影响。

我放代码：

1.我写的代码很垃圾，放的没有意义（主要是时间很紧张，压缩一下应该能在300行左右）。

2.维护学术诚信。

关于Cache的一些思考
#

也不算很深，进一步探究一下，以下都是我自己或者问gpt得到的观点，自己的一些看法，如果您对于某个问题有着更好的理解，欢迎在评论区指出来，这里我说的低级cache或者下层的cache指的是靠近内存的cache。

1.
#

在这个实验中一直强调的一个点是Inclusive policy，这种设计方法在以前的CPU，特别是Intel的CPU中很常见，但其实现代的CPU以及逐渐转向使用NINE模式，因此会产生以下问题：

使用Inclusive policy的缓存必须满足什么条件？这样设计的优缺点分别是什么？

底层缓存必须包含上层的缓存，在底层缓存驱逐的时候要做back invalidation。

好处：

好判断，多核的时候很好知道高级缓存的内容是否存在于低级缓存之中。

缺点：

冗余数据驱逐：L2 驱逐某数据时，即使 L1 正在频繁使用，也必须一并驱逐它，增加了不必要的 L1 miss。

容量浪费：为了维护包含关系，L2 的一些空间可能被迫用于保持与 L1 相同的数据，降低了有效利用率。

降低性能上限：高级缓存未能成为真正的“补充层”，而是受限于 L1 的命中内容。
NINE策略不要求低级cache强制包含高级cache内容，这样做相比inclusive的好处和坏处分别是什么？

（NINE：Non-Inclusive, Non-Exclusive）

NINE就是说下层的cache和上层的cache，二者之间不要求下层cache一定要包含上层cache的内容，同时也不要求两层cache之间的内容一定要是相互排斥的。

好处：

减少了数据冗余，提高了缓存的利用率，当下层的cache要被驱逐的时候，不会影响上层的cache，从而导致没有必要的cache miss。

缺点：

我很难保证一致性的问题，并且数据的管理相对复杂（NINE就是在包含性和排他性策略之间的一种状态），比如说我在L2 cache hit了之后，决定到底要不要把这个数据加载到L1中去之后干掉L2,包含性就是不能干掉，排他性就是必须干掉。
本次实验实际上借助inclusive的性质大大简化了设计，如果采用NINE结构，你将如何调整你的代码？

首先去除back invalidation的这部分逻辑，其次和上一个问题一样，我要设置premote下层cacheline的一个逻辑。

2.
#

现代CPU几乎都采用L1D和L1I两种缓存结构，而在L2及更低级的缓存使用统一指令和数据的方式，这么做的好处是什么？

以下是gpt的回答（我觉得写的还好，是否合理我也就不算很清楚了）：

✅ 为什么 L1 要分成 L1D 和 L1I？

➕ 好处一：提高访问带宽（并行性）

CPU 在每个周期通常同时需要取指（fetch instruction）和访问数据。
如果 L1 是 unified 的，指令和数据会争用同一个缓存端口（cache port）。
分离 L1I 和 L1D 后，CPU 能同时读取指令和访问数据，实现并发访问，提升执行效率。

➕ 好处二：降低访问延迟（latency）

L1 是最靠近执行核心的缓存，需要尽可能小而快。
分开管理指令和数据，可以让 L1I 和 L1D 各自做更有针对性的优化，例如：
- L1I 可以预取、预测分支；
- L1D 可以更好地处理 load/store、写缓冲等。

➕ 好处三：避免污染和干扰

指令和数据的访问模式差异很大：
- 指令访问具有更强的顺序性、局部性好；
- 数据访问则可能跳跃、随机、重复读取。
分开缓存避免了数据污染指令缓存（或反之），提升命中率和稳定性。

✅ 为什么 L2/L3 使用 unified cache？

➕ 原因一：提高缓存利用率

L2/L3 体积更大（通常是几百 KB 到几十 MB）。
如果分为 I-cache 和 D-cache，则可能出现：
- L2D 已满但 L2I 还有空闲空间（或反之）；
- 导致资源浪费。
Unified cache 可以动态地根据访问需求分配空间，更灵活。

➕ 原因二：简化设计，节省成本

L2/L3 远离核心，访问延迟更高，并发访问不再是瓶颈。
统一设计结构更简单，不需要分别维护 tag、替换策略等逻辑。

➕ 原因三：有助于 cache coherence 协议的实现

多核共享的 L3 cache 使用统一结构更方便跟踪、标记和通信，便于维护一致性。

3.
#

你觉得CPU是如何区分指令内存和数据内存的访问的？

1.现代 CPU 内部有清晰划分的模块：

取指单元（Instruction Fetch Unit）专门负责取指令
加载/存储单元（Load/Store Unit）专门负责读写数据

这两者访问内存的路径不同，进而访问不同的 Cache 层次结构（如 L1I vs. L1D）。

2.从软件视角来看：

编译器把「执行代码」转成了存放在某段内存中的机器指令
把「变量数据」分配到另一块内存空间

于是，在 CPU 运行时：

指令指针（PC / IP）发出的访问是“取指”
普通 Load/Store 指令发出的访问是“访问数据”

也就是说根据发出指令的操作单元就可以说明这个指令究竟是I还是L指令。

4.
#

本次实验要求实现严格的LRU算法，一种暴力实现方式是遍历所有cache line, 这样时间复杂度为O（E），你可以设计一种复杂度为O（1）的实现方式吗？

一道关于LRUCahce的lc，你应该能很好的理解为什么？https://leetcode.cn/problems/lru-cache/description/

这是实现的Java代码（我之前写过很多Java代码）

//Least Recently Used
//最近最少使用
//HashMap + DoublyLinkedList
class LRUCache {
    //简单的双向链表
    class Node{
        int key;
        int val;
        Node prev;
        Node next;
        public Node(){}
        public Node(int _key, int _val){key = _key; val = _val;}
    }
    private Map<Integer, Node> cache;
    private int size;
    private int capacity;
    private Node head;
    private Node tail;
    //初始化缓存
    public LRUCache(int capacity) {
        cache = new HashMap<>();
        this.size = 0;
        this.capacity = capacity;
        head = new Node();
        tail = new Node();
        head.next = tail;
        tail.prev = head;
    }
    //相当于读取内存，读取成功这个值就返回value,并且放到双向链表的头部，否则返回-1（实际上要从内存中获取）
    public int get(int key) {
        if(cache.containsKey(key)){
            moveToHead(cache.get(key));
            return cache.get(key).val;
        }
        return -1;
    }
    //写值，道理类似
    public void put(int key, int value) {
        if(cache.containsKey(key)){
            Node node = cache.get(key);
            node.val = value;
            moveToHead(node);
        }else{
            ++size;
            if(size > capacity){
                --size;
                Node d = tail.prev;
                remove(d);
                cache.remove(d.key);
            }
            Node node = new Node(key, value);
            cache.put(key, node);
            add(node);
        }
    }
    //一旦get或者put，就放到head之后，作为最新的节点
    private void moveToHead(Node node){
        remove(node);
        add(node);
    }
    //一旦过容量，或者其他场景，删除节点
    private void remove(Node node){
        Node p = node.prev;
        Node n = node.next;
        p.next = n;
        n.prev = p;
    }
    //新put进来的元素，加到头节点之后
    private void add(Node node){
        Node n = head.next;
        head.next = node;
        node.prev = head;
        node.next = n;
        n.prev = node;
    }
}

基本就是利用；双向链表和hashmap，这样当我们给出一个值，我可以根据这个值直接找到对应的cacheline和在linkedlist中对应的node，直接把这个node提前到head位置，那么这个节点就是最新的，tail之前的节点就是最老的。

虽然是O（1），但是实际的开销并不会小。

5.
#

LRU算法在某种特定的情形下会造成100% miss，你可以发现这种访问模式吗？

LRU Thrashing（LRU抖动）

比如这样，你的L1cache现在只有一个set，三行line，我对于四个元素A B C D进行循环的访问，那么开始就会

依次加入 A B C

接着读取D miss 去除A 放置D

接着读取A miss 去除B 放置A

接着读取B miss 去除 C 放置B

……

上面这样的情况就会100%miss。

6.
#

实际硬件中，实现LRU算法其实十分昂贵，因此大多数厂家采用近似LRU的方法，如果让你设计，你会如何设计这种算法？

来自于gpt，讲的并不好理解，可以看看https://en.wikipedia.org/wiki/Pseudo-LRU

Pseudo-LRU (PLRU)

实现：

最常见的是 二叉树 PLRU（Binary Tree Pseudo LRU）：
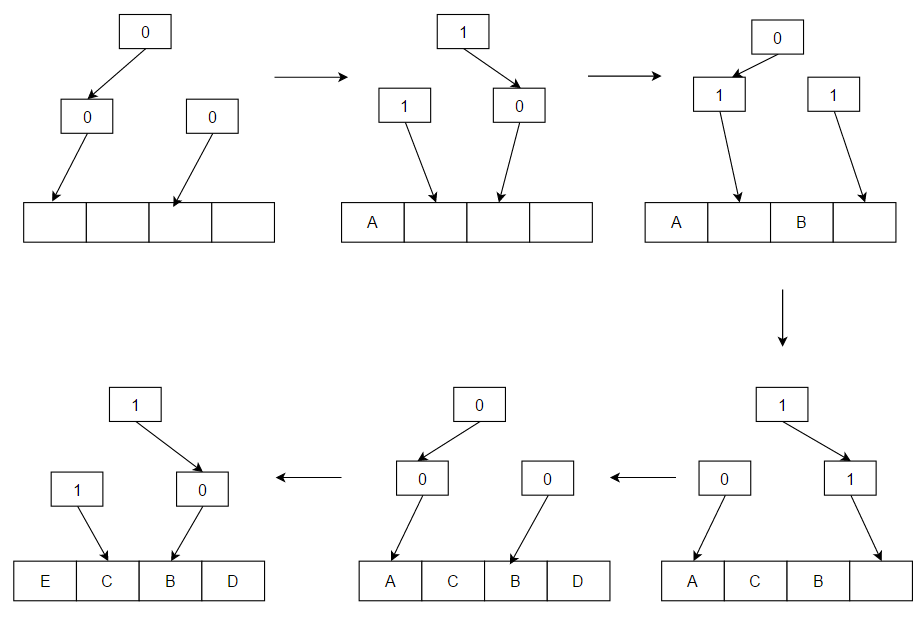
- 适用于 4、8、16 路组相联 Cache。
- 维护一个“树状指针结构”，每个节点记录最近访问的是左还是右。
- 总共只需 E - 1 个 bit 就能表示选择哪条 line 替换。

原理图：

    (b1)
   /   \
(b2)   (b3)
 / \    /  \
A   B  C    D

每个内部节点 0/1 表示最近访问的是哪一侧
选择替换线时，从根节点走向“最久未访问的方向”

举个例子：

b0, b1, b2 是 3 个位（bit），分别控制走向哪个子树。
每个 bit 记录“最近使用的是哪一边”。

这些 bit 可以这样理解：

如果 b0 = 0，表示最近访问的是左子树（A、B），因此优先替换右子树（C、D）
如果 b1 = 1，表示在左子树中，最近访问的是 B → 替换 A
如果 b2 = 0，表示在右子树中，最近访问的是 C → 替换 D

从根开始，按照 bit 的指示往“没被最近访问过”的方向走，直到到达一个叶子节点（就是要被替换的 cache line）。

然后反过来，更新路径上的 bit，表示刚刚走过的那条路径是“最近访问过的”。

假设当前：

b0 = 0 → 上次用了左边（A 或 B）
b1 = 1 → 上次用了 B
b2 = 0 → 上次用了 C

替换时：

从 b0 看 0 → 最近访问的是左边 → 应该替换右边
进入 b2，看 0 → 最近访问的是 C → 应该替换 D

✅ 所以选择替换 D

然后把：

b0 = 1（因为现在访问右边）
b2 = 1（访问了 D）

优点：

硬件实现简单，开销低
实际效果在很多场景下接近 LRU

缺点：

并不是真正的最久未使用，有可能替换到常用块

7.
#

本次实验中在实现上有个小细节是，在发生conflict miss时，我们总是先从下一级fetch数据，然后再判断是否需要evict，这样做的好处和不足是什么？如果上述两个操作的流程互换之后，带来的好处和坏处是什么？你可能需要综合考虑inclusive policy带来的影响。

如果仅有一层cache和memory，那么先后顺序是无所谓的。

我们用两层Cache和memory来理解一下这个问题：

L1 L2 memory

现在我访问L1 miss，L1满了，直接把那个要放入位置的数据驱逐掉。

又访问L2 miss，L2满了，驱逐，此时要考虑back invalidation，如果L1包含，那么那行cacheline也要驱逐掉，但是此时back invalidation的cacheline，和L1时候就驱逐的cacheline有可能是一行cacheline，这是否造成了浪费。

现在再从memory取值放入L2,L1刚刚驱逐的位置。

方案	优点	缺点

先 fetch 后 evict（实验采用）	- 避免 Inclusive 引起的无意义 invalidate - 更稳定一致性 - 实现简单	- 延迟高 - 有时多余 fetch

先 evict 后 fetch	- 可优化延迟 - 有可能并行处理	- 易与 Inclusive 冲突 - 需要额外状态管理

8.
#

进行cache访问时，需要根据内存地址提取出tag，set等字段，而CPU产生的地址实际上都是虚拟地址，需要额外的机制转换成物理地址（详见虚拟内存章节）。因此，cache的设计实际上可以分成physical index和virtual index两种方式，即采用物理地址或者虚拟地址两种地址解析tag，set等内容，那么：

使用physical index的cache的优缺点是什么？

避免了别名的问题，要TLB转换，带来延迟。
使用virtual index的cache的优缺点是什么？

访问会变快，但是有别名的问题。
你能不能设计一种方法综合利用上述两种方式各自的优势？

不能（？）

折中方案：VIPT（Virtual Index, Physical Tag）
#

先用虚拟地址索引（提取 index），用物理地址比对（tag）

优势：
#
- 保留了虚拟访问的速度优势（用虚拟 index 找 set）
- 同时 用物理 tag 避免 alias 问题
- 是 现代 L1 Cache 的主流设计（只要满足 index bits 不跨 page boundary）
设计要点：
#
- Page offset 不变，必须保证 index bits 落在 page offset 范围（否则访问前无法知道 index）。
- 比如：
  - 页大小：4KB = 12 bits offset
  - Index bits ≤ 12
  - Tag 用物理地址中除去 index + block offset 部分

学过一点Java多线程，但是还没有系统学过OS，多少能理解一下多线程的问题，到这里已经相当复杂了，我就不再纸上谈兵了。

9.
#

本次实验中实现的模拟器只能应对顺序访问，如果需要扩展你的模拟器以支持多个线程并发访问，你该如何调整现有的代码？

每一组cacheset用mutex（互斥🔓），保证任何一个时刻，一个set最多仅有一个thread访问。

原子操作LRU等数据。

如果您有更好的看法，欢迎在评论区直接指出！

10.
#

本次实验中不要求考虑多核之间的一致性问题，如果考虑多核之间一致性的问题，且L3作为多核之间的共享缓存，你该如何调整现有的代码？

11.
#

在考虑多核之间cache一致性的前提下，如果需要将inclusive策略变成NINE策略，你需要如何改进现有的代码？

成品代码：

在我的github上也有，在你自己实现的时候会发现很多相似的逻辑，想想怎么封装，本来应该是一个很精妙的代码构成。

#include "cachelab.h"
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
// 可能要包含的头文件
// 要不要封装功能？具体实现的方式
// 先写的时候可以不急着做功能抽象，先写出来试试看
// Q：当我在l2中访问缓存命中时，我要把这个地址加载回l1,但是由于这个地址已经确定，那么不会出现明明有空但是必须驱逐的现象么
// 相关数据统计量，是我在实现的过程中要进行维护的 容易忘记 一共3 * 4 = 12个数据
// 当一个地址给定的时候，它的所有的SetIndex就已经定下来了
// 注意C语言的{}的风格
int l1d_hits = 0;
int l1d_misses = 0;
int l1d_evictions = 0;
int l1i_hits = 0;
int l1i_misses = 0;
int l1i_evictions = 0;
int l2_hits = 0;
int l2_misses = 0;
int l2_evictions = 0;
int l3_hits = 0;
int l3_misses = 0;
int l3_evictions = 0;

// 定义一些常量
#define L1S 2
#define L1B 3

#define L2S 3
#define L2B 3

#define L3S 4
#define L3B 4

#define INSTRUCTION 0
#define DATA 1

//@params time:要使用LRU算法维护的一个全局时钟
int timeStamp = 0;

// 全局变量加载默认初始化为0
void cacheInit()
{
}

// 拼接地址,假设填充的偏移字节不会产生影响：都用0来做填充
// 这里要好好检查有没有出错
uint64_t addressConcate(uint64_t tag, uint64_t setIndex, int s, int b)
{
    uint64_t addr = ((tag << (s + b)) | (setIndex << b));
    return addr;
}

// 把驱逐一个CacheLine的功能封装一下,要考虑无效回溯的情况，但是我很难封装到一个function里面去，最好写成四个function
// 要驱逐的cacheLine地址
// 并且合理利用包含准则
// 直接把地址作为参数，复用性是不是会更强--->我的目的还是为了少传送几个参数
// 这几个驱逐的函数只是单纯的做驱逐的处理，但是不会加载新的值
// lru找要不要也封装？这样对地址操作有可能出错吗？
// 还要对于统计量进行操作
// 要考察是不是无效回溯导致的驱逐，如果是，那么这里不应该算进去统计的问题
// l1i是一个只读的内存,
void evictCacheLineFroml1i(uint64_t evictAddress, bool isBackInvalidation)
{
    uint64_t tag = (evictAddress >> (L1S + L1B));
    uint64_t setIndex = ((evictAddress >> L1B) & 0b11);

    int evictIndex = -1;

    for (int index = 0; index < L1_LINE_NUM; ++index)
    {
        // 找到了要驱逐的行
        if (l1icache[setIndex][index].valid && l1icache[setIndex][index].tag == tag)
        {
            evictIndex = index;
            break;
        }
    }
    // 没有要驱逐的行,因为要考虑Back Invalidation
    if (evictIndex == -1)
    {
        return;
    }
    // 有要驱逐的行
    if (!isBackInvalidation)
    {
        ++l1i_evictions;
    }
    l1icache[setIndex][evictIndex].valid = false;
}

// L1dcache的驱逐的逻辑和L1icahce的逻辑应该是类似的,其实不是
void evictCacheLineFroml1d(uint64_t evictAddress, bool isBackInvalidation)
{
    uint64_t tag = (evictAddress >> (L1S + L1B));
    uint64_t setIndex = ((evictAddress >> L1B) & 0b11);
    int evictIndex = -1;
    for (int index = 0; index < L1_LINE_NUM; ++index)
    {
        // 找到了要驱逐的行
        if (l1dcache[setIndex][index].valid && l1dcache[setIndex][index].tag == tag)
        {
            evictIndex = index;
            break;
        }
    }
    // 没有要驱逐的行,因为要考虑Back Invalidation
    if (evictIndex == -1)
        return;

    if (!isBackInvalidation)
    {
        ++l1d_evictions;
    }
    // 有要驱逐的行
    l1dcache[setIndex][evictIndex].valid = false;
    if (l1dcache[setIndex][evictIndex].dirty)
    {
        uint64_t tag2 = (evictAddress >> (L2S + L2B));
        uint64_t setIndex2 = ((evictAddress >> L2B) & 0b111);
        for (int index = 0; index < L2_LINE_NUM; ++index)
        {
            if (l2ucache[setIndex2][index].valid && l2ucache[setIndex2][index].tag == tag2)
            {
                // L2的这个Cache被写了，更改timeStamp
                ++l2_hits;
                ++timeStamp;
                l2ucache[setIndex2][index].latest_used = timeStamp;
                l2ucache[setIndex2][index].dirty = true;
                return;
            }
        }
    }
}

// 从l2ucache驱逐,还要考虑你驱逐的是i还是d
void evictCacheLineFroml2(uint64_t evictAddress, int TYPE, bool isBackInvalidation)
{
    if (!isBackInvalidation)
    {
        uint64_t tag = (evictAddress >> (L2S + L2B));
        uint64_t setIndex = ((evictAddress >> L2B) & 0b111);
        int evictIndex = -1;
        for (int index = 0; index < L2_LINE_NUM; ++index)
        {
            if (l2ucache[setIndex][index].valid && l2ucache[setIndex][index].tag == tag)
            {
                evictIndex = index;
            }
        }
        // 没有找到要驱逐的位置
        if (evictIndex == -1)
        {
            return;
        }
        // 这里要进行驱逐
        // 首先从l2ucache驱逐要考虑无效回溯
        // L2 back Invalidation L1的时候不应该给L1算一次evict?
        ++l2_evictions;
        evictCacheLineFroml1d(evictAddress, true);
        evictCacheLineFroml1i(evictAddress, true);
        l2ucache[setIndex][evictIndex].valid = false;

        // 直接驱逐的情况
        if (l2ucache[setIndex][evictIndex].dirty)
        {
            uint64_t tag3 = (evictAddress >> (L3S + L3B));
            uint64_t setIndex3 = ((evictAddress >> L3B) & 0b1111);
            for (int index = 0; index < L3_LINE_NUM; ++index)
            {
                if (l3ucache[setIndex3][index].valid && l3ucache[setIndex3][index].tag == tag3)
                {
                    ++l3_hits;
                    ++timeStamp;
                    l3ucache[setIndex3][index].latest_used = timeStamp;
                    l3ucache[setIndex3][index].dirty = true;
                    return;
                }
            }
        }
    }
    else
    {
        uint64_t tag = (evictAddress >> (L2S + L2B));
        uint64_t setIndex = ((evictAddress >> L2B) & 0b111);
        int evictIndex = -1;
        for (int index = 0; index < L2_LINE_NUM; ++index)
        {
            if (l2ucache[setIndex][index].valid && l2ucache[setIndex][index].tag == tag)
            {
                evictIndex = index;
                evictCacheLineFroml1d(evictAddress, true);
                evictCacheLineFroml1i(evictAddress, true);
                l2ucache[setIndex][evictIndex].valid = false;
                // 直接驱逐的情况
                if (l2ucache[setIndex][evictIndex].dirty)
                {
                    uint64_t tag3 = (evictAddress >> (L3S + L3B));
                    uint64_t setIndex3 = ((evictAddress >> L3B) & 0b1111);
                    for (int i = 0; i < L3_LINE_NUM; ++i)
                    {
                        if (l3ucache[setIndex3][i].valid && l3ucache[setIndex3][i].tag == tag3)
                        {
                            ++l3_hits;
                            ++timeStamp;
                            l3ucache[setIndex3][i].latest_used = timeStamp;
                            l3ucache[setIndex3][i].dirty = true;
                        }
                    }
                }
            }
        }

        if (setIndex % 2 == 0)
        {
            ++setIndex;
            evictIndex = -1;
            for (int index = 0; index < L2_LINE_NUM; ++index)
            {
                if (l2ucache[setIndex][index].valid && l2ucache[setIndex][index].tag == tag)
                {
                    evictIndex = index;
                    evictCacheLineFroml1d(evictAddress, true);
                    evictCacheLineFroml1i(evictAddress, true);
                    l2ucache[setIndex][evictIndex].valid = false;
                    // 直接驱逐的情况
                    if (l2ucache[setIndex][evictIndex].dirty)
                    {
                        uint64_t tag3 = (evictAddress >> (L3S + L3B));
                        uint64_t setIndex3 = ((evictAddress >> L3B) & 0b1111);
                        for (int i = 0; i < L3_LINE_NUM; ++i)
                        {
                            if (l3ucache[setIndex3][i].valid && l3ucache[setIndex3][i].tag == tag3)
                            {
                                ++l3_hits;
                                ++timeStamp;
                                l3ucache[setIndex3][i].latest_used = timeStamp;
                                l3ucache[setIndex3][i].dirty = true;
                            }
                        }
                    }
                }
            }
        }

        if (setIndex % 2 == 1)
        {
            --setIndex;
            evictIndex = -1;
            for (int index = 0; index < L2_LINE_NUM; ++index)
            {
                if (l2ucache[setIndex][index].valid && l2ucache[setIndex][index].tag == tag)
                {
                    evictIndex = index;
                    evictCacheLineFroml1d(evictAddress, true);
                    evictCacheLineFroml1i(evictAddress, true);
                    l2ucache[setIndex][evictIndex].valid = false;
                    // 直接驱逐的情况
                    if (l2ucache[setIndex][evictIndex].dirty)
                    {
                        uint64_t tag3 = (evictAddress >> (L3S + L3B));
                        uint64_t setIndex3 = ((evictAddress >> L3B) & 0b1111);
                        for (int i = 0; i < L3_LINE_NUM; ++i)
                        {
                            if (l3ucache[setIndex3][i].valid && l3ucache[setIndex3][i].tag == tag3)
                            {
                                ++l3_hits;
                                ++timeStamp;
                                l3ucache[setIndex3][i].latest_used = timeStamp;
                                l3ucache[setIndex3][i].dirty = true;
                            }
                        }
                    }
                }
            }
        }
    }
}

// 从l3ucache驱逐，同样要考虑驱逐的类型问题
void evictCacheLineFroml3(uint64_t evictAddress, int TYPE)
{
    uint64_t tag = (evictAddress >> (L3S + L3B));
    uint64_t setIndex = ((evictAddress >> L3B) & 0b1111);
    int evictIndex = -1;
    for (int index = 0; index < L3_LINE_NUM; ++index)
    {
        if (l3ucache[setIndex][index].valid && l3ucache[setIndex][index].tag == tag)
        {
            evictIndex = index;
            break;
        }
    }

    if (evictIndex == -1)
    {
        return;
    }

    // Back Invalidation
    ++l3_evictions;
    evictCacheLineFroml2(evictAddress, INSTRUCTION, true);

    l3ucache[setIndex][evictIndex].valid = false;
}

// TODO：思考fetch函数组的封装有没有问题
// 想把一个line从L2fetch到l1i
void fetchl2tol1i(uint64_t setIndex1, uint64_t tag1)
{
    // 维护l1驱逐的情况
    int evictIndexl1i = -1;
    uint64_t minTimeStampl1i = UINT64_MAX;
    for (int j = 0; j < L1_LINE_NUM; ++j)
    {
        // 能找到L1也存在无效的情况,最好的情况
        if (!l1icache[setIndex1][j].valid)
        {
            ++timeStamp;
            l1icache[setIndex1][j].latest_used = timeStamp;
            l1icache[setIndex1][j].dirty = false;
            l1icache[setIndex1][j].tag = tag1;
            l1icache[setIndex1][j].valid = true;
            return;
        }
        // 要给l1驱逐的情况
        else
        {
            if (l1icache[setIndex1][j].latest_used < minTimeStampl1i)
            {
                minTimeStampl1i = l1icache[setIndex1][j].latest_used;
                evictIndexl1i = j;
            }
        }
    }
    // 先给l1i做驱逐
    uint64_t evictL1iAddress = addressConcate(l1icache[setIndex1][evictIndexl1i].tag, setIndex1, L1S, L1B);
    evictCacheLineFroml1i(evictL1iAddress, false);
    // 此时l1i已经驱逐完毕,驱逐完了之后再fetch进去
    ++timeStamp;
    l1icache[setIndex1][evictIndexl1i].latest_used = timeStamp;
    l1icache[setIndex1][evictIndexl1i].dirty = false;
    l1icache[setIndex1][evictIndexl1i].tag = tag1;
    l1icache[setIndex1][evictIndexl1i].valid = true;
}

// 把一个line从L2fetch到l1d
void fetchl2tol1d(uint64_t setIndex1, uint64_t tag1)
{
    int evictIndexl1d = -1;
    uint64_t minTimeStampl1d = UINT64_MAX;
    for (int j = 0; j < L1_LINE_NUM; ++j)
    {
        if (!l1dcache[setIndex1][j].valid)
        {
            ++timeStamp;
            l1dcache[setIndex1][j].latest_used = timeStamp;
            l1dcache[setIndex1][j].dirty = false;
            l1dcache[setIndex1][j].tag = tag1;
            l1dcache[setIndex1][j].valid = true;
            return;
        }
        else
        {
            if (l1dcache[setIndex1][j].latest_used < minTimeStampl1d)
            {
                minTimeStampl1d = l1dcache[setIndex1][j].latest_used;
                evictIndexl1d = j;
            }
        }
    }
    uint64_t evictL1dAddress = addressConcate(l1dcache[setIndex1][evictIndexl1d].tag, setIndex1, L1S, L1B);
    evictCacheLineFroml1d(evictL1dAddress, false);
    ++timeStamp;
    l1dcache[setIndex1][evictIndexl1d].latest_used = timeStamp;
    l1dcache[setIndex1][evictIndexl1d].dirty = false;
    l1dcache[setIndex1][evictIndexl1d].tag = tag1;
    l1dcache[setIndex1][evictIndexl1d].valid = true;
}

// 把一个line从L3fetch到L2
void fetchl3tol2(uint64_t setIndex2, uint64_t tag2, int TYPE)
{
    uint64_t minTimeStamp = UINT64_MAX;
    // 如果满了，要驱逐的index
    int evictIndex = -1;
    for (int i = 0; i < L2_LINE_NUM; ++i)
    {
        if (!l2ucache[setIndex2][i].valid)
        {
            ++timeStamp;
            l2ucache[setIndex2][i].latest_used = timeStamp;
            l2ucache[setIndex2][i].dirty = false;
            l2ucache[setIndex2][i].tag = tag2;
            l2ucache[setIndex2][i].valid = true;
            return;
        }
        else
        {
            if (l2ucache[setIndex2][i].latest_used < minTimeStamp)
            {
                minTimeStamp = l2ucache[setIndex2][i].latest_used;
                evictIndex = i;
            }
        }
    }
    // 考虑L2的驱逐
    uint64_t evictaddressl2 = addressConcate(l2ucache[setIndex2][evictIndex].tag, setIndex2, L2S, L2B);
    evictCacheLineFroml2(evictaddressl2, TYPE, false);
    ++timeStamp;
    l2ucache[setIndex2][evictIndex].latest_used = timeStamp;
    l2ucache[setIndex2][evictIndex].dirty = false;
    l2ucache[setIndex2][evictIndex].tag = tag2;
    l2ucache[setIndex2][evictIndex].valid = true;
}

// 把一个内存中的值fetch到l3
void fetchMemoryTol3(uint64_t setIndex3, uint64_t tag3, int TYPE)
{
    int evictIndex = -1;
    uint64_t minTimeStamp = UINT64_MAX;
    for (int index = 0; index < L3_LINE_NUM; ++index)
    {
        if (!l3ucache[setIndex3][index].valid)
        {
            ++timeStamp;
            l3ucache[setIndex3][index].latest_used = timeStamp;
            l3ucache[setIndex3][index].dirty = false;
            l3ucache[setIndex3][index].tag = tag3;
            l3ucache[setIndex3][index].valid = true;
            return;
        }
        else
        {
            if (l3ucache[setIndex3][index].latest_used < minTimeStamp)
            {
                minTimeStamp = l3ucache[setIndex3][index].latest_used;
                evictIndex = index;
            }
        }
    }
    uint64_t evictAddress = addressConcate(l3ucache[setIndex3][evictIndex].tag, setIndex3, L3S, L3B);
    evictCacheLineFroml3(evictAddress, TYPE);
    ++timeStamp;
    l3ucache[setIndex3][evictIndex].latest_used = timeStamp;
    l3ucache[setIndex3][evictIndex].dirty = false;
    l3ucache[setIndex3][evictIndex].tag = tag3;
    l3ucache[setIndex3][evictIndex].valid = true;
}

/* 我们先写一个Instruction尝试一下:读取指令
 * @params addr 为访问地址，它是trace文件中的地址的十进制表示的结果,64位16进制内存地址
 * OK：经过纯I指令检测，这个函数实现的没有问题
 */
void instruct(uint64_t addr)
{
    // 先访问第一级Cache,处理addr
    uint64_t tag1 = (addr >> (L1S + L1B));
    uint64_t setIndex1 = ((addr >> L1B) & 0b11);

    uint64_t tag2 = (addr >> (L2S + L2B));
    uint64_t setIndex2 = ((addr >> L2B) & 0b111);

    uint64_t tag3 = (addr >> (L3S + L3B));
    uint64_t setIndex3 = ((addr >> L3B) & 0b1111);

    //  根据拿到的数据看第一级有没有命中
    for (int index = 0; index < L1_LINE_NUM; ++index)
    {
        // 合法并且tag相同，就是命中
        if (l1icache[setIndex1][index].valid && l1icache[setIndex1][index].tag == tag1)
        {
            // 命中之后的处理
            ++timeStamp;
            ++l1i_hits;
            l1icache[setIndex1][index].latest_used = timeStamp;
            return;
        }
    }

    // 到这里证明l1i没有命中,在l2中找
    ++l1i_misses;
    for (int index = 0; index < L2_LINE_NUM; ++index)
    {
        // l2中缓存命中
        if (l2ucache[setIndex2][index].valid && l2ucache[setIndex2][index].tag == tag2)
        {
            ++timeStamp;
            l2ucache[setIndex2][index].latest_used = timeStamp;
            ++l2_hits;
            fetchl2tol1i(setIndex1, tag1);
            return;
        }
    }

    // 到这里证明l2没有命中，在l3中找
    ++l2_misses;
    for (int index = 0; index < L3_LINE_NUM; ++index)
    {
        // l3缓存命中
        if (l3ucache[setIndex3][index].valid && l3ucache[setIndex3][index].tag == tag3)
        {
            ++timeStamp;
            l3ucache[setIndex3][index].latest_used = timeStamp;
            ++l3_hits;
            fetchl3tol2(setIndex2, tag2, INSTRUCTION);
            fetchl2tol1i(setIndex1, tag1);
            return;
        }
    }

    // 到这里证明l3没有命中，要从缓存中取值加载到三层里面去
    ++l3_misses;
    // 找要驱逐的L3的地址
    fetchMemoryTol3(setIndex3, tag3, INSTRUCTION);
    fetchl3tol2(setIndex2, tag2, INSTRUCTION);
    fetchl2tol1i(setIndex1, tag1);
    // 理论上到这里取值令的过程已经结束
}

// 读取数据的问题,读取数据和读取指令是否是类似的
void load(uint64_t addr)
{
    // 先访问第一级Cache,处理addr
    uint64_t tag1 = (addr >> (L1S + L1B));
    uint64_t setIndex1 = ((addr >> L1B) & 0b11);

    uint64_t tag2 = (addr >> (L2S + L2B));
    uint64_t setIndex2 = ((addr >> L2B) & 0b111);

    uint64_t tag3 = (addr >> (L3S + L3B));
    uint64_t setIndex3 = ((addr >> L3B) & 0b1111);

    //  根据拿到的数据看第一级有没有命中
    for (int index = 0; index < L1_LINE_NUM; ++index)
    {
        // 合法并且tag相同，就是命中
        if (l1dcache[setIndex1][index].valid && l1dcache[setIndex1][index].tag == tag1)
        {
            // 命中之后的处理
            ++timeStamp;
            ++l1d_hits;
            l1dcache[setIndex1][index].latest_used = timeStamp;
            return;
        }
    }

    ++l1d_misses;
    for (int index = 0; index < L2_LINE_NUM; ++index)
    {
        // l2中缓存命中
        if (l2ucache[setIndex2][index].valid && l2ucache[setIndex2][index].tag == tag2)
        {
            ++timeStamp;
            l2ucache[setIndex2][index].latest_used = timeStamp;
            ++l2_hits;
            fetchl2tol1d(setIndex1, tag1);
            return;
        }
    }

    // 到这里证明l2没有命中，在l3中找
    ++l2_misses;
    for (int index = 0; index < L3_LINE_NUM; ++index)
    {
        // l3缓存命中
        if (l3ucache[setIndex3][index].valid && l3ucache[setIndex3][index].tag == tag3)
        {
            ++timeStamp;
            l3ucache[setIndex3][index].latest_used = timeStamp;
            ++l3_hits;
            fetchl3tol2(setIndex2, tag2, DATA);
            fetchl2tol1d(setIndex1, tag1);
            return;
        }
    }

    // 到这里证明l3没有命中，要从缓存中取值加载到三层里面去
    ++l3_misses;
    // 找要驱逐的L3的地址
    fetchMemoryTol3(setIndex3, tag3, DATA);
    fetchl3tol2(setIndex2, tag2, DATA);
    fetchl2tol1d(setIndex1, tag1);
}

// 重点逻辑：写入内存的实现
// 先fetch这个cacheline，接着才进行改动，我这里成了先改动，再fecth上去，肯定是不行的
// 简单来说，写入操作是不会影响L2和L3的
void store(uint64_t addr)
{
    // 先列出所有可能要访问的数据
    uint64_t tag1 = (addr >> (L1S + L1B));
    uint64_t setIndex1 = ((addr >> L1B) & 0b11);

    uint64_t tag2 = (addr >> (L2S + L2B));
    uint64_t setIndex2 = ((addr >> L2B) & 0b111);

    uint64_t tag3 = (addr >> (L3S + L3B));
    uint64_t setIndex3 = ((addr >> L3B) & 0b1111);

    // 写l1d
    for (int index = 0; index < L1_LINE_NUM; ++index)
    {
        // l1d write hit
        if (l1dcache[setIndex1][index].valid && l1dcache[setIndex1][index].tag == tag1)
        {
            ++l1d_hits;
            ++timeStamp;
            l1dcache[setIndex1][index].latest_used = timeStamp;
            l1dcache[setIndex1][index].dirty = true;
            return;
        }
    }

    // l1d write misses
    ++l1d_misses;

    // 在L2中写
    for (int index = 0; index < L2_LINE_NUM; ++index)
    {
        // l2 write hit
        if (l2ucache[setIndex2][index].valid && l2ucache[setIndex2][index].tag == tag2)
        {
            // L2写命中，我先把这个位置加载回l1d，接着才进行dirty的修改，写命中时，首先更改一下lru
            ++l2_hits;
            ++timeStamp;
            l2ucache[setIndex2][index].latest_used = timeStamp;
            fetchl2tol1d(setIndex1, tag1);
            for (int i = 0; i < L1_LINE_NUM; ++i)
            {
                // 在fetch了之后，此时这里的lru已经发生了改变，所以是不是不用再进行更改?
                // 应该是的
                if (l1dcache[setIndex1][i].valid && l1dcache[setIndex1][i].tag == tag1)
                {
                    l1dcache[setIndex1][i].dirty = true;
                    return;
                }
            }
        }
    }

    // l2u write misses
    ++l2_misses;
    for (int index = 0; index < L3_LINE_NUM; ++index)
    {
        // l3 write hit
        if (l3ucache[setIndex3][index].valid && l3ucache[setIndex3][index].tag == tag3)
        {
            ++l3_hits;
            ++timeStamp;
            l3ucache[setIndex3][index].latest_used = timeStamp;
            fetchl3tol2(setIndex2, tag2, DATA);
            fetchl2tol1d(setIndex1, tag1);
            for (int i = 0; i < L1_LINE_NUM; ++i)
            {
                if (l1dcache[setIndex1][i].valid && l1dcache[setIndex1][i].tag == tag1)
                {
                    l1dcache[setIndex1][i].dirty = true;
                    return;
                }
            }
        }
    }

    // l3u write miss,在内存中写，然后直接加载上去，是否正确,显然错误
    ++l3_misses;
    fetchMemoryTol3(setIndex3, tag3, DATA);
    fetchl3tol2(setIndex2, tag2, DATA);
    fetchl2tol1d(setIndex1, tag1);
    // 在fetch完了之后，在set1中找要写的值，接着写入即可
    for (int i = 0; i < L1_LINE_NUM; ++i)
    {
        if (l1dcache[setIndex1][i].valid && l1dcache[setIndex1][i].tag == tag1)
        {
            l1dcache[setIndex1][i].dirty = true;
            return;
        }
    }
}

// you are not allowed to modify the declaration of this function
/*cacheAccess函数接受三个参数，参数的定义为：
 * 而且我们不考虑byte的个数，我们这个函数只是模拟访问内存的操作，不实际读写数据
 *@params op 为访问类型，是一个char类型的参数，具体取值和trace文件中的类型相同，为[I, S, L，M]其中的一个。
 *@params addr 为访问地址，它是trace文件中的地址的十进制表示的结果,64位16进制内存地址
 *@params len 为一次访问的长度，也就是字节数量
 *   思考过程：
 *   1.怎么处理地址？要根据不同缓存级别的组数用不同的方式来解读地址么？然后剩下的位都是tag标志
 *   2.I是指令加载的过程，和数据读取类似，但是一级缓存中只能从L1I中来读取指令数据
 *   3.M修改数据，就是一次Load加上一次Store Load：就是读取 Store：就是写入数据
 *   4.代码框架大概是怎样的？一个对应的指令实现一个功能？
 */
void cacheAccess(char op, uint64_t addr, uint32_t len)
{
    switch (op)
    {
    case 'I':
        instruct(addr);
        break;
    case 'M':
        load(addr);
        store(addr);
        break;
    case 'L':
        load(addr);
        break;
    case 'S':
        store(addr);
        break;
    default:
        break;
    }
}

Author

mio

I’m Just A Student…

CSAPP:CacheLab #

CacheLine的组织方式 #

处理写操作的方法 #

多级cache的包含准则(inclusion policy) #

三级Cache模拟器 #

关于Cache的一些思考 #

1. #

2. #

3. #

4. #

5. #

6. #

7. #

8. #

折中方案：VIPT（Virtual Index, Physical Tag） #

优势： #

设计要点： #

9. #

10. #

11. #